题目内容
8．在多边形内角和公式的探究过程中，主要运用的数学思想是（ ）| A． | 化归思想 | B． | 分类讨论 | C． | 方程思想 | D． | 数形结合思想 |
分析 多边形内角和定理：（n-2）•180 （n≥3）且n为整数）此公式推导的基本方法是从n边形的一个顶点出发引出（n-3）条对角线，将n边形分割为（n-2）个三角形，这（n-2）个三角形的所有内角之和正好是n边形的内角和，体现了化归思想．
解答 解：因为多边形内角和公式推导的基本方法是从n边形的一个顶点出发引出（n-3）条对角线，将n边形分割为（n-2）个三角形，这（n-2）个三角形的所有内角之和正好是n边形的内角和，体现了化归思想．
故选A．
点评 本题主要考查了在数学的学习过程，主要体现的数学思想有哪些，弄清推导过程是解答此题的关键．
练习册系列答案
阅读快车系列答案
相关题目
18．
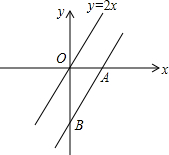如图，把直线y=2x向下平移后得到直线AB，直线AB与x轴、y轴分别相交于点A、B．若△ABO的面积是1，则直线AB的解析式是（ ）
如图，把直线y=2x向下平移后得到直线AB，直线AB与x轴、y轴分别相交于点A、B．若△ABO的面积是1，则直线AB的解析式是（ ）| A． | y=3x+$\sqrt{2}$ | B． | y=2x-$\sqrt{2}$ | C． | y=3x-2 | D． | y=2x-2 |
16．为了促进湖北省的经济发展，省政府提出了总计约为1.2万亿元的投资计划，将1.2万亿用科学记数法表示应为（ ）
| A． | 1.2×1010 | B． | 1.2×1011 | C． | 1.2×1012 | D． | 1.2×1013 |
3．下列等式成立的是（ ）
| A． | $\sqrt{7}$-$\sqrt{2}$=$\sqrt{5}$ | B． | $\sqrt{2}$×$\sqrt{3}$=$\sqrt{6}$ | C． | $\sqrt{{2}^{2}+{3}^{2}}$=5 | D． | -$\sqrt{（-5）^{2}}$=5 |
20．计算（2ab2）3，结果正确的是（ ）
| A． | 2a3b6 | B． | 6a3b6 | C． | 8a3b5 | D． | 8a3b6 |