题目内容
在△ABC中,AC=BC,点O为底边AB中点,点D为AC腰上一点,连接BD,过点C作CE⊥BD,垂足为点E,连结EO.
(1)如图1,求证:∠OEB=
∠ACB;
(2)如图2,当∠ACB=90°时,连接AE,若∠AEO=90°,请你探究线段DE与EO之间的数量关系,并证明你的结论.

(1)如图1,求证:∠OEB=
| 1 |
| 2 |
(2)如图2,当∠ACB=90°时,连接AE,若∠AEO=90°,请你探究线段DE与EO之间的数量关系,并证明你的结论.

考点:四点共圆,等腰三角形的性质,直角三角形斜边上的中线,圆周角定理,相似三角形的判定与性质
专题:证明题
分析:(1)取BC的中点P,连接PO、PE、CO,如图1.要证∠OEB=
∠ACB,只需证∠OEB=∠BCO,只需证C、E、O、B四点共圆,只需证PE=PO=PC=PB即可.
(2)过点A作AM⊥BD于M,过点O作ON⊥BD于N,连接CO,如图2.由C、E、O、B四点共圆可得∠OEB=45°,从而可得AE=
AM=
EM,EO=
EN=
ON.易证△BNO∽△BMA,根据相似三角形的性质可得AM=2ON,进而有AE=2EO.易证△AMD∽△AEO,根据相似三角形的性质可得AM=2DM,就可得到MD=ED=
ME=
AM=ON,进而有EO=
ON=
ED.
| 1 |
| 2 |
(2)过点A作AM⊥BD于M,过点O作ON⊥BD于N,连接CO,如图2.由C、E、O、B四点共圆可得∠OEB=45°,从而可得AE=
| 2 |
| 2 |
| 2 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 2 |
| 2 |
解答:解:(1)证明:取BC的中点P,连接PO、PE、CO,如图1.
∵CA=CB,点O是AB的中点,
∴∠ACO=∠BCO=
∠ACB,CO⊥AB.
∵CE⊥DB,CO⊥AB,
∴∠CEB=∠COB=90°.
∵点P是BC的中点,
∴PE=PO=PC=PB=
BC,
∴点C、E、O、B在以点P为圆心,PO为半径的圆上,
∴∠OEB=∠BCO,
∴∠OEB=
∠ACB.
(2)EO=
DE.
证明:过点A作AM⊥BD于M,过点O作ON⊥BD于N,连接CO,如图2.
∵C、E、O、B四点共圆,
∴∠OEB=∠BCO=
∠ACB=45°.
∵AM⊥BD,ON⊥BD,
∴∠AME=∠ONE=90°,
∴∠MAE=∠MEA=∠EON=∠OEN=45°,
∴AE=
AM=
EM,EO=
EN=
ON.
∵∠AME=∠ONB=90°,
∴ON∥AM,
∴△BNO∽△BMA,
∴
=
=
,
∴AM=2ON,
∴AE=2EO.
∵∠MAE=∠CAO=45°,
∴∠MAD=∠EAO.
∵∠M=∠AEO=90°,
∴△AMD∽△AEO,
∴
=
=2,
∴AM=2DM,
∴AM=ME=2DM,
∴MD=ED=
ME=
AM=ON,
∴EO=
ON=
ED.
∵CA=CB,点O是AB的中点,
∴∠ACO=∠BCO=
| 1 |
| 2 |

∵CE⊥DB,CO⊥AB,
∴∠CEB=∠COB=90°.
∵点P是BC的中点,
∴PE=PO=PC=PB=
| 1 |
| 2 |
∴点C、E、O、B在以点P为圆心,PO为半径的圆上,
∴∠OEB=∠BCO,
∴∠OEB=
| 1 |
| 2 |
(2)EO=
| 2 |
证明:过点A作AM⊥BD于M,过点O作ON⊥BD于N,连接CO,如图2.
∵C、E、O、B四点共圆,
∴∠OEB=∠BCO=
| 1 |
| 2 |
∵AM⊥BD,ON⊥BD,
∴∠AME=∠ONE=90°,
∴∠MAE=∠MEA=∠EON=∠OEN=45°,

∴AE=
| 2 |
| 2 |
| 2 |
| 2 |
∵∠AME=∠ONB=90°,
∴ON∥AM,
∴△BNO∽△BMA,
∴
| ON |
| AM |
| OB |
| AB |
| 1 |
| 2 |
∴AM=2ON,
∴AE=2EO.
∵∠MAE=∠CAO=45°,
∴∠MAD=∠EAO.
∵∠M=∠AEO=90°,
∴△AMD∽△AEO,
∴
| AM |
| DM |
| AE |
| OE |
∴AM=2DM,
∴AM=ME=2DM,
∴MD=ED=
| 1 |
| 2 |
| 1 |
| 2 |
∴EO=
| 2 |
| 2 |
点评:本题主要考查了四点共圆的判定、圆周角定理、相似三角形的判定与性质、等腰三角形的性质、直角三角形斜边上的中线等于斜边的一半、勾股定理等知识,综合性比较强,难度比较大,证到∠OEB=45°及△AMD∽△AEO是解决第(2)小题的关键.

练习册系列答案
 导学全程练创优训练系列答案
导学全程练创优训练系列答案
相关题目
下列几组数中互为相反数的是( )
A、-
| ||
B、
| ||
| C、-(-6)和6 | ||
D、-
|
(-1)2009+(-1)2010的值是( )
| A、-2 | B、-1 | C、0 | D、1 |
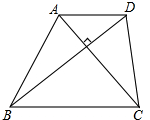 如图,在四边形ABCD中,AD∥BC,且AD<BC,AC、BD为两条对角线,且AC⊥BD,AC=BD.
如图,在四边形ABCD中,AD∥BC,且AD<BC,AC、BD为两条对角线,且AC⊥BD,AC=BD.