题目内容
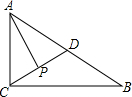 △ABC中,AC=3,BC=4,AB=5,D是AB中点,点P由C沿CD方向运动,每秒钟移1个单位,若△APD的面积为y,点P移动时间为x秒,
△ABC中,AC=3,BC=4,AB=5,D是AB中点,点P由C沿CD方向运动,每秒钟移1个单位,若△APD的面积为y,点P移动时间为x秒,(1)求y与x之间的函数关系式;
(2)多少秒后△APD的面积为2.4?
考点:一次函数的应用,三角形的面积,勾股定理的逆定理
专题:几何动点问题
分析:(1)先在△ABC中,由AC=3,BC=4,AB=5,根据勾股定理的逆定理得出∠ACB=90°,再由D是AB中点,根据直角三角形斜边上的中线等于斜边的一半得出CD=
AB=2.5.设△ACD中CD边上的高为h.根据三角形中线的性质可知S△ACD=
S△ABC,由此列出方程
×2.5h=
×
×4×3,求出h=2.4.再根据CP=1•x=x,PD=CD-CP=2.5-x,根据三角形的面积公式即可求出y与x之间的函数关系式;
(2)将y=2.4代入(1)中所求的关系式,解方程即可.
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
(2)将y=2.4代入(1)中所求的关系式,解方程即可.
解答:解:(1)∵△ABC中,AC=3,BC=4,AB=5,
∴AC2+BC2=AB2,
∴∠ACB=90°,
∵D是AB中点,
∴CD=
AB=2.5.
设△ACD中CD边上的高为h.
∵S△ACD=
S△ABC,
∴
×2.5h=
×
×4×3,
∴h=2.4.
∵CP=1•x=x,
∴PD=CD-CP=2.5-x,
∴y=
(2.5-x)×2.4=
-
x,
即y与x之间的函数关系式为y=
-
x;
(2)当△APD的面积为2.4时,
-
x=2.4,
解得x=0.4.
故0.4秒后△APD的面积为2.4.
∴AC2+BC2=AB2,
∴∠ACB=90°,
∵D是AB中点,
∴CD=
| 1 |
| 2 |
设△ACD中CD边上的高为h.
∵S△ACD=
| 1 |
| 2 |
∴
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
∴h=2.4.
∵CP=1•x=x,
∴PD=CD-CP=2.5-x,
∴y=
| 1 |
| 2 |
| 72 |
| 25 |
| 6 |
| 5 |
即y与x之间的函数关系式为y=
| 72 |
| 25 |
| 6 |
| 5 |
(2)当△APD的面积为2.4时,
| 72 |
| 25 |
| 6 |
| 5 |
解得x=0.4.
故0.4秒后△APD的面积为2.4.
点评:本题考查了一次函数的应用,勾股定理的逆定理,直角三角形的性质,三角形中线的性质,三角形的面积,代数式求值,难度适中.求出△ACD中CD边上的高是解题的关键.

练习册系列答案
相关题目
 如图,请添加一个条件:
如图,请添加一个条件: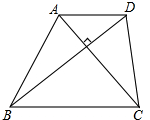 如图,在四边形ABCD中,AD∥BC,且AD<BC,AC、BD为两条对角线,且AC⊥BD,AC=BD.
如图,在四边形ABCD中,AD∥BC,且AD<BC,AC、BD为两条对角线,且AC⊥BD,AC=BD. 将正整数按如图所示的规律排列下去.若用有序数对(n,m)表示第n排,从左到右第m个数,如(4,3)表示整数9,则(17,2)表示的数是
将正整数按如图所示的规律排列下去.若用有序数对(n,m)表示第n排,从左到右第m个数,如(4,3)表示整数9,则(17,2)表示的数是