Question

【题目】如图（1），某数学活动小组经探究发现：在⊙O中，直径AB与弦CD相交于点P,此时PA· PB=PC·PD

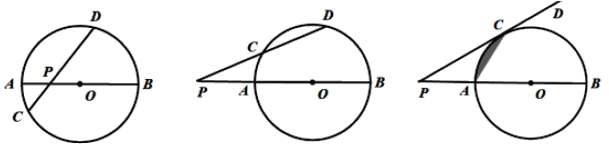
（1）如图（2），若AB与CD相交于圆外一点P, 上面的结论是否成立？请说明理由．

（2）如图（3）,将PD绕点P逆时针旋转至与⊙O相切于点C, 直接写出PA、PB、PC之间的数量关系．

（3）如图（3），直接利用（2）的结论，求当 PC= ,PA=1时,阴影部分的面积．

Answer 1

【答案】（1）成立，理由见解析；（2）；（3）

【解析】

（1）连接AD、BC，得到∠D=∠B，可证△PAD∽△PCB，即可求解；

（2）根据（1）中的结论即可求解；

（3）连接OC，根据 ,PC= ,PA=1求出PB=3 , AO=CO=1，PO=2 利用,得到AOC为等边三角形，再分别求出，即可求解.

解：（1）成立

理由如下：如图，连接AD、BC

则∠D=∠B

∵∠P=∠P

∴△PAD∽△PCB

∴=

∴PA· PB=PC·PD

(2)当PD与⊙O相切于点C时，

PC=PD，

由（1）得PA· PB=PC·PD

∴

(3)如图，连接OC

,PC= ,PA=1

PB=3 , AO=CO=1，PO=2

PC与 ⊙O相切于点C

PCO为直角三角形

,

AOC为等边三角形

=

==

=