ĢāÄæÄŚČŻ
”¾ĢāÄæ”æ×ŪŗĻÓėĢ½¾æ
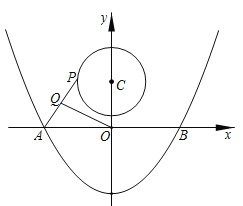
ČēĶ¼£¬Å×ĪļĻß![]() ¾¹żµćA(-2,0)£¬B(4,0)Į½µć£¬Óė
¾¹żµćA(-2,0)£¬B(4,0)Į½µć£¬Óė![]() Öį½»ÓŚµćC£¬µćDŹĒÅ×ĪļĻßÉĻŅ»øö¶Æµć£¬ÉčµćDµÄŗį×ų±źĪŖ
Öį½»ÓŚµćC£¬µćDŹĒÅ×ĪļĻßÉĻŅ»øö¶Æµć£¬ÉčµćDµÄŗį×ų±źĪŖ![]() .Į¬½ÓAC£¬BC£¬DB£¬DC£¬
.Į¬½ÓAC£¬BC£¬DB£¬DC£¬
(1)ĒóÅ×ĪļĻßµÄŗÆŹż±ķ“ļŹ½£»
(2)”÷BCDµÄĆ껿µČÓŚ”÷AOCµÄĆ껿µÄ![]() Ź±£¬Ēó
Ź±£¬Ēó![]() µÄÖµ£»
掙术
(3)ŌŚ(2)µÄĢõ¼žĻĀ£¬ČōµćMŹĒ![]() ÖįÉĻµÄŅ»øö¶Æµć£¬µćNŹĒÅ×ĪļĻßÉĻŅ»¶Æµć£¬ŹŌÅŠ¶ĻŹĒ·ń“ęŌŚÕāŃłµÄµćM,Ź¹µĆŅŌµćB£¬D£¬M£¬NĪŖ¶„µćµÄĖıߊĪŹĒĘ½ŠŠĖıߊĪ£¬Čō“ęŌŚ£¬ĒėÖ±½ÓŠ“³öµćMµÄ×ų±ź£»Čō²»“ęŌŚ£¬ĒėĖµĆ÷ĄķÓÉ.
ÖįÉĻµÄŅ»øö¶Æµć£¬µćNŹĒÅ×ĪļĻßÉĻŅ»¶Æµć£¬ŹŌÅŠ¶ĻŹĒ·ń“ęŌŚÕāŃłµÄµćM,Ź¹µĆŅŌµćB£¬D£¬M£¬NĪŖ¶„µćµÄĖıߊĪŹĒĘ½ŠŠĖıߊĪ£¬Čō“ęŌŚ£¬ĒėÖ±½ÓŠ“³öµćMµÄ×ų±ź£»Čō²»“ęŌŚ£¬ĒėĖµĆ÷ĄķÓÉ.

”¾“š°ø”æ(1)![]() £»(2)3£»(3)
£»(2)3£»(3)![]() .
.
”¾½āĪö”æ
(1)ĄūÓĆ“ż¶ØĻµŹż·Ø½ųŠŠĒó½ā¼“æÉ£»
(2)×÷Ö±ĻßDE”Ķ![]() ÖįÓŚµćE£¬½»BCÓŚµćG£¬×÷CF”ĶDE£¬“¹×ćĪŖF£¬ĻČĒó³öS”÷OAC=6£¬ŌŁøł¾ŻS”÷BCD=
ÖįÓŚµćE£¬½»BCÓŚµćG£¬×÷CF”ĶDE£¬“¹×ćĪŖF£¬ĻČĒó³öS”÷OAC=6£¬ŌŁøł¾ŻS”÷BCD=![]() S”÷AOC£¬µĆµ½S”÷BCD =
S”÷AOC£¬µĆµ½S”÷BCD =![]() £¬Č»ŗóĒó³öBCµÄ½āĪöŹ½ĪŖ
£¬Č»ŗóĒó³öBCµÄ½āĪöŹ½ĪŖ![]() £¬ŌņæɵƵćGµÄ×ų±źĪŖ
£¬ŌņæɵƵćGµÄ×ų±źĪŖ![]() £¬ÓÉ“ĖæɵĆ
£¬ÓÉ“ĖæɵĆ![]() £¬ŌŁøł¾ŻS”÷BCD=S”÷CDG+S”÷BDG=
£¬ŌŁøł¾ŻS”÷BCD=S”÷CDG+S”÷BDG=![]() £¬æÉµĆ¹ŲÓŚmµÄ·½³Ģ£¬½ā·½³Ģ¼“æÉĒóµĆ“š°ø£»
£¬æÉµĆ¹ŲÓŚmµÄ·½³Ģ£¬½ā·½³Ģ¼“æÉĒóµĆ“š°ø£»
(3)“ęŌŚ£¬ČēĻĀĶ¼ĖłŹ¾£¬ŅŌBDĪŖ±ß»ņÕßŅŌBDĪŖ¶Ō½ĒĻß½ųŠŠĘ½ŠŠĖıߊĪµÄ¹¹Ķ¼£¬ŅŌBDĪŖ±ßŹ±£¬ÓŠ3ÖÖĒéæö£¬ÓɵćDµÄ×ų±źæɵƵćNµćׯ×ų±źĪŖ”Ą![]() £¬Č»ŗó·ÖµćNµÄׯ×ų±źĪŖ
£¬Č»ŗó·ÖµćNµÄׯ×ų±źĪŖ![]() ŗĶµćNµÄׯ×ų±źĪŖ
ŗĶµćNµÄׯ×ų±źĪŖ![]() Į½ÖÖĒéæö·Ö±šĒó½ā£»ŅŌBDĪŖ¶Ō½ĒĻߏ±£¬ÓŠ1ÖÖĒéæö£¬“ĖŹ±N1µćÓėN2µćÖŲŗĻ£¬øł¾ŻĘ½ŠŠĖıߊĪµÄ¶Ō±ßĘ½ŠŠĒŅĻąµČæÉĒóµĆBM1=N1D=4£¬¼Ģ¶ųĒóµĆOM1= 8£¬ÓÉ“Ė¼“æÉĒóµĆ“š°ø.
Į½ÖÖĒéæö·Ö±šĒó½ā£»ŅŌBDĪŖ¶Ō½ĒĻߏ±£¬ÓŠ1ÖÖĒéæö£¬“ĖŹ±N1µćÓėN2µćÖŲŗĻ£¬øł¾ŻĘ½ŠŠĖıߊĪµÄ¶Ō±ßĘ½ŠŠĒŅĻąµČæÉĒóµĆBM1=N1D=4£¬¼Ģ¶ųĒóµĆOM1= 8£¬ÓÉ“Ė¼“æÉĒóµĆ“š°ø.
(1)Å×ĪļĻß![]() ¾¹żµćA(-2,0)£¬B(4,0)£¬
¾¹żµćA(-2,0)£¬B(4,0)£¬
”ą![]() £¬
£¬
½āµĆ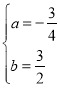 £¬
£¬
”ąÅ×ĪļĻßµÄŗÆŹż±ķ“ļŹ½ĪŖ![]() £»
£»
(2)×÷Ö±ĻßDE”Ķ![]() ÖįÓŚµćE£¬½»BCÓŚµćG£¬×÷CF”ĶDE£¬“¹×ćĪŖF£¬
ÖįÓŚµćE£¬½»BCÓŚµćG£¬×÷CF”ĶDE£¬“¹×ćĪŖF£¬
”ßµćAµÄ×ų±źĪŖ(-2,0)£¬”ąOA=2£¬
ÓÉ![]() £¬µĆ
£¬µĆ![]() £¬”ąµćCµÄ×ų±źĪŖ(0,6)£¬”ąOC=6£¬
£¬”ąµćCµÄ×ų±źĪŖ(0,6)£¬”ąOC=6£¬
”ąS”÷OAC=![]() £¬
£¬
”ßS”÷BCD=![]() S”÷AOC£¬
S”÷AOC£¬
”ąS”÷BCD =![]() £¬
£¬
ÉčÖ±ĻßBCµÄŗÆŹż±ķ“ļŹ½ĪŖ![]() £¬
£¬
ÓÉB£¬CĮ½µćµÄ×ų±źµĆ![]() £¬½āµĆ
£¬½āµĆ £¬
£¬
”ąÖ±ĻßBCµÄŗÆŹż±ķ“ļŹ½ĪŖ![]() £¬
£¬
”ąµćGµÄ×ų±źĪŖ![]() £¬
£¬
”ą![]() £¬
£¬
”ßµćBµÄ×ų±źĪŖ(4,0)£¬”ąOB=4£¬
”ßS”÷BCD=S”÷CDG+S”÷BDG=![]() £¬
£¬
”ąS”÷BCD =![]() £¬
£¬
”ą![]() £¬
£¬
½āµĆ![]() (Éį)£¬
(Éį)£¬![]() £¬
£¬
”ą![]() µÄÖµĪŖ3£»
µÄÖµĪŖ3£»
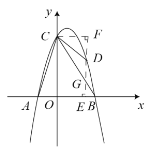
(3)“ęŌŚ£¬ČēĻĀĶ¼ĖłŹ¾£¬ŅŌBDĪŖ±ß»ņÕßŅŌBDĪŖ¶Ō½ĒĻß½ųŠŠĘ½ŠŠĖıߊĪµÄ¹¹Ķ¼£¬
ŅŌBDĪŖ±ßŹ±£¬ÓŠ3ÖÖĒéæö£¬
”ßDµć×ų±źĪŖ![]() £¬”ąµćNµćׯ×ų±źĪŖ”Ą
£¬”ąµćNµćׯ×ų±źĪŖ”Ą![]() £¬
£¬
µ±µćNµÄׯ×ų±źĪŖ![]() Ź±£¬ČēµćN2£¬
Ź±£¬ČēµćN2£¬
“ĖŹ±![]() £¬½āµĆ£ŗ
£¬½āµĆ£ŗ![]() (Éį)£¬
(Éį)£¬
”ą![]() £¬”ą
£¬”ą![]() £»
£»
µ±µćNµÄׯ×ų±źĪŖ![]() Ź±£¬ČēµćN3£¬N4£¬
Ź±£¬ČēµćN3£¬N4£¬
“ĖŹ±![]() £¬½āµĆ£ŗ
£¬½āµĆ£ŗ![]()
”ą![]() £¬
£¬![]() £¬
£¬
”ą![]() £¬
£¬![]() £»
£»
ŅŌBDĪŖ¶Ō½ĒĻߏ±£¬ÓŠ1ÖÖĒéæö£¬“ĖŹ±N1µćÓėN2µćÖŲŗĻ£¬
”ß![]() £¬D(3£¬
£¬D(3£¬![]() )£¬
)£¬
”ąN1D=4£¬
”ąBM1=N1D=4£¬
”ąOM1=OB+BM1=8£¬
”ąM1(8£¬0)£¬
×ŪÉĻ£¬µćMµÄ×ų±źĪŖ£ŗ![]() .
.