题目内容
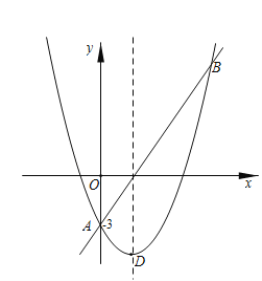
【题目】如图，直线AB和抛物线的交点是A（0，﹣3），B（5，9），已知抛物线的顶点D的横坐标是2．
（1）求抛物线的解析式及顶点坐标；
（2）在x轴上是否存在一点C，与A，B组成等腰三角形？若存在，求出点C的坐标，若不在，请说明理由；
【答案】（1）抛物线的解析式为：y＝
x2﹣
x﹣3，顶点D的坐标为（2，﹣
）；
（2）存在，C坐标为：（4
，0）或（﹣4，0），（5+
，0）或（5﹣2
，0），（
，0），
【解析】
（1）根据抛物线的顶点D的横坐标为2，可设抛物线的解析式为
，再将点A和B的坐标代入即可得；
（2）先求出AB的长，然后分哪两条边为等腰
的腰，设点C的坐标为
，根据两腰相等，利用两点之间距离公式建立等式，求解即可.
（1）抛物线的顶点D的横坐标为2，可设抛物线的解析式为：
将
代入得
解得：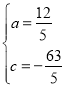
则抛物线的解析式为：
（或写成一般形式
）
由顶点式可得顶点D的坐标为
；
（ 2）设点C坐标
因
则
①当
时，则
解得：
，即点C坐标为：
或
②当
时，则
解得：
，即点C坐标为
或
③当
时，则
解得：
，即点C坐标为
综上，存在这样的点C，点C的坐标为或或或或.
练习册系列答案
相关题目
【题目】抛物线
上部分点的横坐标
，纵坐标
的对应值如下表：
| … | -2 | -1 | 0 | 1 | 2 | … |
| … | 0 | 4 | 6 | 6 | 4 | … |
从上表可知，下列说法中正确的是______.（填写序号）
①抛物线与轴的一个交点为
； ②函数的最大值为6；
③抛物线的对称轴是直线
； ④在对称轴左侧，随增大而增大.
