题目内容
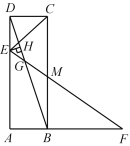
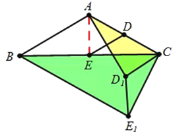
【题目】如图①,在![]() 中,
中,![]() ,
,![]() ,点
,点![]() 、
、![]() 分别是
分别是![]() 、
、![]() 的中点,连接
的中点,连接![]() .
.

(1)在图①中,![]() 的值为______;
的值为______;![]() 的值为______.
的值为______.
(2)若将![]() 绕点
绕点![]() 逆时针方向旋转得到
逆时针方向旋转得到![]() ,点
,点![]() 、
、![]() 的对应点为
的对应点为![]() 、
、![]() ,在旋转过程中
,在旋转过程中![]() 的大小是否发生变化?请仅就图②的情形给出证明.
的大小是否发生变化?请仅就图②的情形给出证明.
(3)当![]() 在旋转一周的过程中,
在旋转一周的过程中,![]() ,
,![]() ,
,![]() 三点共线时,请你直接写出线段
三点共线时,请你直接写出线段![]() 的长.
的长.
【答案】(1) ![]() ;
;![]() ;(2) 不发生变化,理由见解析;(3)
;(2) 不发生变化,理由见解析;(3)![]() 或
或![]()
【解析】
(1)根据直角三角形30°角的性质即可解决问题;
(2)只要证明![]() ,根据相似三角形的性质即可得
,根据相似三角形的性质即可得![]() 的值即可;
的值即可;
(3)分当点![]() 在线段
在线段![]() 上时及当点
上时及当点![]() 在线段
在线段![]() 的延长线上时,两种情况画出图形分别解决即可.
的延长线上时,两种情况画出图形分别解决即可.
(1)在图①中,连接![]() ,
,
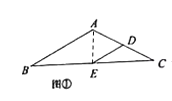
∵![]() ,点
,点![]() 分别是
分别是![]() 的中点,
的中点,
∴![]() ,
,
∴![]() ,
,
∵![]() ,
,![]() ,
,
∴![]() ,
,
在![]() 中,
中,![]() ,
,![]() ,
,
∵点![]() 是
是![]() 的中点,
的中点,
∴![]() ,
,
∴![]() ;
;![]() .
.
(2)解:不发生变化.
连接![]() ,
,
∵![]() ,点
,点![]() 分别是
分别是![]() 的中点,
的中点,
∴![]() ,
,
∴![]() ,
,
∵![]() ,
,![]() ,
,
∴![]() ,
,
在![]() 中,
中,![]() ,
,![]() ,
,
∵点![]() 是
是![]() 的中点,
的中点,
∴![]() ,
,![]() .
.
∵点![]() 是
是![]() 的中点,
的中点,
∴![]() ,
,
∵旋转,
∴![]() ,
,![]() ,
,![]() ,
,
∴![]() ;
;![]() ,
,![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() .
.
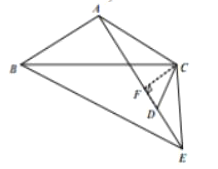
(3)由旋转可知:在△CDE中,∠CDE=120°,DE=CD=1,由(1)可知![]()
如图,作CF⊥AE,
∵∠CDE=120°
∴∠CDF=60°,
在Rt△CDF中:![]() ,
,![]()
在Rt△ADF中:![]() ,
,
∴![]() ,
,
∴![]()
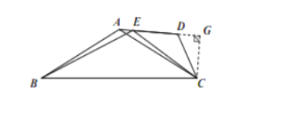
如图,作CG⊥AE,
∵∠CDE=120°
∴∠CDG=60° ,
在Rt△CDF中:![]() ,
,![]() ,
,
在Rt△ADF中:![]() ,
,
∴![]() ,
,
∴![]()

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目