题目内容
 如图:Rt△ABC,∠C=90°,BC=6cm,AC=8cm,将△BCD沿BD折叠,使C落在AB边上的C′处,求S△ADC′.
如图:Rt△ABC,∠C=90°,BC=6cm,AC=8cm,将△BCD沿BD折叠,使C落在AB边上的C′处,求S△ADC′.考点:翻折变换(折叠问题)
专题:
分析:利用勾股定理列式求出AB,根据折叠的性质可得BC′=BC,CD=C′D,∠BC′D=∠C=90°,然后求出AC′,设C′D=CD=x,表示出AD,再利用勾股定理列出方程求出x,然后利用三角形的面积公式列式计算即可得解.
解答:解:∵BC=6cm,AC=8cm,
∴AB=
=
=10cm,
∵△BCD沿BD折叠,C落在AB边上的C′处,
∴BC′=BC=6cm,CD=C′D,∠BC′D=∠C=90°,
∴AC′=AB-BC′=10-6=4cm,
设C′D=CD=x,则AD=8-x,
在Rt△AC′D中,AD2=AC′2+C′D2,
即(8-x)2=42+x2,
解得x=3,
所以,C′D=3cm,
∴S△ADC′=
×4×3=6cm2.
∴AB=
| AC2+BC2 |
| 82+62 |
∵△BCD沿BD折叠,C落在AB边上的C′处,
∴BC′=BC=6cm,CD=C′D,∠BC′D=∠C=90°,
∴AC′=AB-BC′=10-6=4cm,
设C′D=CD=x,则AD=8-x,
在Rt△AC′D中,AD2=AC′2+C′D2,
即(8-x)2=42+x2,
解得x=3,
所以,C′D=3cm,
∴S△ADC′=
| 1 |
| 2 |
点评:本题考查了翻折变换的性质,勾股定理,主要利用了翻折前后的两个图形对应边相等,对应角相等,利用勾股定理列出方程求出C′D的长度是解题的关键.

练习册系列答案
 愉快的寒假南京出版社系列答案
愉快的寒假南京出版社系列答案
相关题目
下列运算正确的是( )
A、
| ||||
B、(
| ||||
| C、(-a2)3=a6 | ||||
D、a6÷(
|
下列运算正确的是( )
| A、(2a)2=2a2 |
| B、2a+3a=5a |
| C、a2•a3=a6 |
| D、﹙a2﹚3=a5 |
 如图,在平面直角坐标系中,已知四边形ABCD的四个顶点坐标为A(0,6)、B(-3,0)、C(0,-2)、D(4,0),P为AB、DC延长线的交点.
如图,在平面直角坐标系中,已知四边形ABCD的四个顶点坐标为A(0,6)、B(-3,0)、C(0,-2)、D(4,0),P为AB、DC延长线的交点. 已知,AB、AC是圆O的切线,B、C是切点,BD是圆O的直径,连接AO、CD,
已知,AB、AC是圆O的切线,B、C是切点,BD是圆O的直径,连接AO、CD,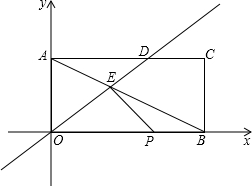 如图,矩形AOBC在直角坐标系中,已知点A的坐标为(0,3),点B的坐标为(6,0),直线y=
如图,矩形AOBC在直角坐标系中,已知点A的坐标为(0,3),点B的坐标为(6,0),直线y= 如图,将长方形纸片ABCD折叠,使边DC落在对角线AC上,折痕为CE,且D点落在对角线D′处.若AB=3,AD=4,则ED的长为
如图,将长方形纸片ABCD折叠,使边DC落在对角线AC上,折痕为CE,且D点落在对角线D′处.若AB=3,AD=4,则ED的长为