题目内容
 已知,AB、AC是圆O的切线,B、C是切点,BD是圆O的直径,连接AO、CD,
已知,AB、AC是圆O的切线,B、C是切点,BD是圆O的直径,连接AO、CD,(1)求证:OA∥CD;
(2)过D点作AC的平行线,分别交AB、AO于E、F,若AB=BD,求tan∠BDE的值.
考点:切线的性质
专题:计算题
分析:(1)连接BC,交OA于点G,根据AB,AC为圆O的切线,利用切线长定理得到AB=AC,AO为角平分线,利用三线合一得到AG垂直于BC,利用同角的余角相等得到一对内错角角相等,利用内错角相等两直线平行即可得证;
(2)由DE与AC平行,利用两直线平行内错角相等得到一对角相等,再由AO为角平分线得到一对角相等,等量代换得到∠AFE=∠EAF,利用外角的性质得到∠BED=2∠EAF,在直角三角形ABD中,利用锐角三角函数定义求出tan∠EAF的值,利用二倍角的正切函数公式求出tan∠BED的值,即可确定出tan∠BDE的值.
(2)由DE与AC平行,利用两直线平行内错角相等得到一对角相等,再由AO为角平分线得到一对角相等,等量代换得到∠AFE=∠EAF,利用外角的性质得到∠BED=2∠EAF,在直角三角形ABD中,利用锐角三角函数定义求出tan∠EAF的值,利用二倍角的正切函数公式求出tan∠BED的值,即可确定出tan∠BDE的值.
解答: 解:(1)连接BC,交OA于点G,
解:(1)连接BC,交OA于点G,
∵AB、AC是圆O的切线,B、C是切点,
∴AB=AC,AO为∠CAB的平分线,
∴AG⊥BC,
∴∠GOC+∠GCO=90°,
∵BD为圆O的直径,
∴∠BCD=90°,
∴∠GCO+∠OCD=90°,
∴∠GOC=∠OCD,
∴OA∥CD;
(2)∵DE∥AC,
∴∠AFE=∠CAF,
∵∠EAF=∠CAF,
∴∠AFE=∠EAF,
∴∠BED=2∠EAF,
∵AB=BD,O为BD的中点,
∴tan∠BAO=
,
∴tan∠BED=
=
,
则tan∠BDE=
.
 解:(1)连接BC,交OA于点G,
解:(1)连接BC,交OA于点G,∵AB、AC是圆O的切线,B、C是切点,
∴AB=AC,AO为∠CAB的平分线,
∴AG⊥BC,
∴∠GOC+∠GCO=90°,
∵BD为圆O的直径,
∴∠BCD=90°,
∴∠GCO+∠OCD=90°,
∴∠GOC=∠OCD,
∴OA∥CD;
(2)∵DE∥AC,
∴∠AFE=∠CAF,
∵∠EAF=∠CAF,
∴∠AFE=∠EAF,
∴∠BED=2∠EAF,
∵AB=BD,O为BD的中点,
∴tan∠BAO=
| 1 |
| 2 |
∴tan∠BED=
| 2tan∠BAO |
| 1-tan2∠BAO |
| 4 |
| 3 |
则tan∠BDE=
| 3 |
| 4 |
点评:此题考查了切线的性质,切线长定理,平行线的判定与性质,以及锐角三角函数定义,熟练掌握切线的性质是解本题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
下列式子正确的是( )
| A、-1<-100 | ||||
B、-
| ||||
C、2<
| ||||
| D、0>π |
 一个由棱长都是1的小正方体组成的立体图形的三视图如图,则它的表面积为( )
一个由棱长都是1的小正方体组成的立体图形的三视图如图,则它的表面积为( )| A、10 | B、12 | C、14 | D、20 |
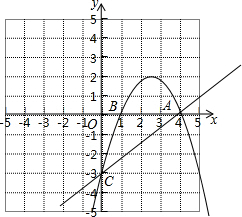 已知抛物线y=-
已知抛物线y=- 如图,直线AB、CD被直线EF所截,如果同位角∠1=∠3,那么内错角∠2与∠3相等吗?同旁内角∠3与∠5互补吗?请说明理由.
如图,直线AB、CD被直线EF所截,如果同位角∠1=∠3,那么内错角∠2与∠3相等吗?同旁内角∠3与∠5互补吗?请说明理由. 如图:Rt△ABC,∠C=90°,BC=6cm,AC=8cm,将△BCD沿BD折叠,使C落在AB边上的C′处,求S△ADC′.
如图:Rt△ABC,∠C=90°,BC=6cm,AC=8cm,将△BCD沿BD折叠,使C落在AB边上的C′处,求S△ADC′. 如图,△ABC中,AB=AC,D是△ABC内一点,连接AD、BD、CD,∠ADB=∠ADC,求证:DB=DC.
如图,△ABC中,AB=AC,D是△ABC内一点,连接AD、BD、CD,∠ADB=∠ADC,求证:DB=DC.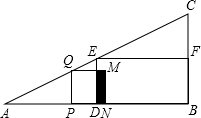 已知:在Rt△ABC中,∠B=90°,BC=4cm,AB=8cm,D、E、F分别为AB、AC、BC边上的中点.若P为AB边上的一个动点,PQ∥BC,且交AC于点Q,以PQ为一边,在点A的异侧作正方形PQMN,记正方形PQMN与矩形EDBF的公共部分的面积为y.当y=2cm2时,试确定点P的位置.
已知:在Rt△ABC中,∠B=90°,BC=4cm,AB=8cm,D、E、F分别为AB、AC、BC边上的中点.若P为AB边上的一个动点,PQ∥BC,且交AC于点Q,以PQ为一边,在点A的异侧作正方形PQMN,记正方形PQMN与矩形EDBF的公共部分的面积为y.当y=2cm2时,试确定点P的位置. 有A、B、C三家工厂依次坐落在一条笔直的公路边,甲、乙两辆运货卡车分别从A、B工厂同时出发,沿公路匀速驶向C工厂,最终到达C工厂.设甲、乙两辆卡车行驶x (h)后,与B工厂的距离分别为y1、y2 (km),y1、y2与x的函数关系如图所示,根据图象解答下列问题.(提示:图中较粗的折线表示的是y与x的函数关系.)
有A、B、C三家工厂依次坐落在一条笔直的公路边,甲、乙两辆运货卡车分别从A、B工厂同时出发,沿公路匀速驶向C工厂,最终到达C工厂.设甲、乙两辆卡车行驶x (h)后,与B工厂的距离分别为y1、y2 (km),y1、y2与x的函数关系如图所示,根据图象解答下列问题.(提示:图中较粗的折线表示的是y与x的函数关系.)