题目内容
2.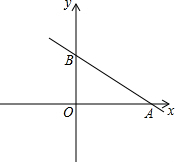 如图,在直角坐标系xOy中,O为坐标原点,直线y=kx-$\sqrt{3}$k+3交y轴正半轴于点B,交x轴于点A.
如图,在直角坐标系xOy中,O为坐标原点,直线y=kx-$\sqrt{3}$k+3交y轴正半轴于点B,交x轴于点A.(1)试说明点C($\sqrt{3}$,3)一定在直线AB上;
(2)试探索:当原点O到直线AB的距离取得最大值时,
①求出此时直线AB的解析式;
②在第一象限内的点P,满足△POB与△ABO相似.请直接写出所有符合条件的点P的坐标.(不必写出解答过程)
分析 (1)根据已知条件得到当x=$\sqrt{3}$时,y=k×$\sqrt{3}$-$\sqrt{3}$k+3=3,即可得到结论;
(2)①当OC⊥AB时,点O到直线AB的距离最大,如图1,过点C任作一条异于直线AB的直线DE,并过点O作OF⊥DE于点F,则在Rt△△OCF中,斜边OC>OF,于是得到当点C与F重合,即OC⊥AB时,点O到直线AB的距离最大,此时OC=$\sqrt{(0-\sqrt{3})^{2}+(0-3)^{2}}$=2$\sqrt{3}$,如图2,过点C作CD⊥x轴于点D,由C($\sqrt{3}$,3),则∠COD=60°在Rt△AOC中,∠CAO=30°,OC=2$\sqrt{3}$,求得OA=4$\sqrt{3}$,得到A(4$\sqrt{3}$,0),代入即可得到结论;
②当∠OBP=90°时,如图3,(Ⅰ)若△BOP∽△BAO,则∠BOP=∠BAO=30°,解直角三角形得到BP=$\frac{\sqrt{3}}{3}$OB=$\frac{4\sqrt{3}}{3}$,求得P2($\frac{4\sqrt{3}}{3}$,4),(Ⅱ)若△BPO∽△BAO,则∠BPO=∠BAO=30°,解直角三角形得到BP=$\sqrt{3}$OB=4$\sqrt{3}$,求得P1(4$\sqrt{3}$,4);当∠OPB=90°时(Ⅲ)过点P作OP⊥BA于点P,如图4,此时△PBO∽△OBA,∠BOP=∠BAO=30°过点P作PM⊥OA于点M.在Rt△PBO中,根据直角三角形的性质得到BP=$\frac{1}{2}$OB=2,OP=$\sqrt{3}$BP=2$\sqrt{3}$,在Rt△PMO中,∠OPM=30°,根据直角三角形的性质得到OM=$\frac{1}{2}$OP=$\sqrt{3}$,PM=$\sqrt{3}$OM=3,求得P3($\sqrt{3}$,3),(Ⅳ)若△POB∽△OBA,如图4,则∠OBP=∠BAO=30°,∠POM=30°.解直角三角形得到PM=$\frac{\sqrt{3}}{3}$OM=1,求得P4($\sqrt{3}$,1),当∠POB=90°时,点P在x轴上,不符合要求.
解答 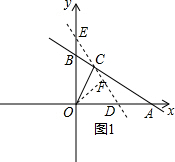 解:(1)依题意,得
解:(1)依题意,得
当x=$\sqrt{3}$时,y=k×$\sqrt{3}$-$\sqrt{3}$k+3=3,
∴点C($\sqrt{3}$,3)一定在直线AB上;
(2)①当OC⊥AB时,点O到直线AB的距离最大,
如图1,过点C任作一条异于直线AB的直线DE,并过点O作OF⊥DE于点F,
则在Rt△△OCF中,斜边OC>OF,
∴当点C与F重合,即OC⊥AB时,点O到直线AB的距离最大,
此时OC=$\sqrt{(0-\sqrt{3})^{2}+(0-3)^{2}}$=2$\sqrt{3}$,
如图2,过点C作CD⊥x轴于点D,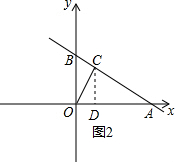
∵C($\sqrt{3}$,3),则∠COD=60°
在Rt△AOC中,∠CAO=30°,OC=2$\sqrt{3}$,
∴OA=4$\sqrt{3}$,图1
∴A(4$\sqrt{3}$,0),
∴0=4$\sqrt{3}$k-$\sqrt{3}$k+3解得k=-$\frac{\sqrt{3}}{3}$,
∴直线AB的解析式为y=-$\frac{\sqrt{3}}{3}$x+4;
②当∠OBP=90°时,如图3,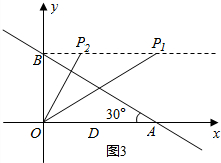 (Ⅰ)若△BOP∽△BAO,
(Ⅰ)若△BOP∽△BAO,
则∠BOP=∠BAO=30°,BP=$\frac{\sqrt{3}}{3}$OB=$\frac{4\sqrt{3}}{3}$,
∴P2($\frac{4\sqrt{3}}{3}$,4),
(Ⅱ)若△BPO∽△BAO,
则∠BPO=∠BAO=30°,BP=$\sqrt{3}$OB=4$\sqrt{3}$,
∴P1(4$\sqrt{3}$,4);
当∠OPB=90°时
(Ⅲ)过点P作OP⊥BA于点P,如图4,
此时△PBO∽△OBA,∠BOP=∠BAO=30°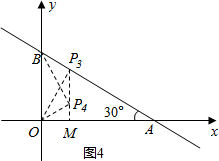
过点P作PM⊥OA于点M.
在Rt△PBO中,BP=$\frac{1}{2}$OB=2,
OP=$\sqrt{3}$BP=2$\sqrt{3}$,
∵在Rt△PMO中,∠OPM=30°,
∴OM=$\frac{1}{2}$OP=$\sqrt{3}$,PM=$\sqrt{3}$OM=3,
∴P3($\sqrt{3}$,3),
(Ⅳ)若△POB∽△OBA,如图4,
则∠OBP=∠BAO=30°,∠POM=30°.
∴PM=$\frac{\sqrt{3}}{3}$OM=1,
∴P4($\sqrt{3}$,1),
当∠POB=90°时,点P在x轴上,不符合要求.
综合得,符合条件的点有四个,分别是p2($\frac{4}{3}\sqrt{3}$,4),p1(4$\sqrt{3}$,4),p3($\sqrt{3}$,3),p4($\sqrt{3}$,1).
点评 本题综合考查了用待定系数法求一次函数的解析式和相似三角形的有关知识,解决这类问题常用到分类讨论、数形结合、方程和转化等数学思想方法.

 新非凡教辅冲刺100分系列答案
新非凡教辅冲刺100分系列答案| A. | 在三个偶数中任选一个能被2整除 | |
| B. | 两个有理数相除,结果是无理数 | |
| C. | 一个四边形的内角和是560° | |
| D. | 用一个平面去截圆柱体,得到的截面是矩形 |
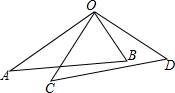 如图所示,将一副三角板叠放在一起,使直角顶点重合,且∠AOD=2∠BOC,则∠AOC的等于( )
如图所示,将一副三角板叠放在一起,使直角顶点重合,且∠AOD=2∠BOC,则∠AOC的等于( )| A. | 45° | B. | 30° | C. | 25° | D. | 20° |
| A. | $\sqrt{3}$ | B. | 3.14 | C. | $\frac{11}{7}$ | D. | $-\root{3}{0.001}$ |

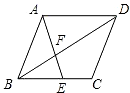 如图,平行四边形ABCD中,E是边BC上的点,AE交BD于点F,如果$\frac{BE}{EC}=\frac{3}{2}$,那么$\frac{{{S_{△BEF}}}}{{{S_{△DAF}}}}$=$\frac{9}{25}$.
如图,平行四边形ABCD中,E是边BC上的点,AE交BD于点F,如果$\frac{BE}{EC}=\frac{3}{2}$,那么$\frac{{{S_{△BEF}}}}{{{S_{△DAF}}}}$=$\frac{9}{25}$.