题目内容
14.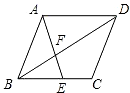 如图,平行四边形ABCD中,E是边BC上的点,AE交BD于点F,如果$\frac{BE}{EC}=\frac{3}{2}$,那么$\frac{{{S_{△BEF}}}}{{{S_{△DAF}}}}$=$\frac{9}{25}$.
如图,平行四边形ABCD中,E是边BC上的点,AE交BD于点F,如果$\frac{BE}{EC}=\frac{3}{2}$,那么$\frac{{{S_{△BEF}}}}{{{S_{△DAF}}}}$=$\frac{9}{25}$.
分析 由平行四边形的性质和已知条件BE:CE=3:2,可求出BE:AD=3:5,易证△BEF∽△DAF,再由相似三角形的性质即可求出两个三角形的面积比.
解答 解:∵四边形ABCD是平行四边形,
∴AD∥BC,AD=BC,
∴△BEF∽△DAF,
∴BF:FD=BE:AD,
又∵BE:EC=3:2,
∴BE:BC=3:5,
∴BE:AD=3:5,
∴$\frac{{{S_{△BEF}}}}{{{S_{△DAF}}}}$=$\frac{9}{25}$
故答案为$\frac{9}{25}$.
点评 本题考查了平行四边形的性质及相似三角形的判定与性质,熟练掌握平行于三角形一边的直线和其他两边(或两边的延长线)相交,所构成的三角形与原三角形相似是解题关键.

练习册系列答案
相关题目
9.二元一次方程组$\left\{\begin{array}{l}{2x+y=10}\\{x=2y}\end{array}\right.$的解是( )
| A. | $\left\{\begin{array}{l}{x=4}\\{y=3}\end{array}\right.$ | B. | $\left\{\begin{array}{l}{x=6}\\{y=3}\end{array}\right.$ | C. | $\left\{\begin{array}{l}{x=4}\\{y=2}\end{array}\right.$ | D. | $\left\{\begin{array}{l}{x=2}\\{y=4}\end{array}\right.$ |
19.下列图形中,既是轴对称,又是中心对称图形的是( )
| A. |  | B. |  | C. |  | D. |  |
6.股民张智慧上星期五买进某公司1000股,每股27元,下表为本周每日该股票的涨跌情况.(单位:元)
(1)星期四收盘时,每股是多少元?
(2)本周内最高价是每股多少元?最低价是多少元?
(3)已知张智慧买进时付了0.15%的手续费,卖出时须付成交额0.15%的手续费和0.1%的交易税,如果张智慧在星期五收盘前将全部股票卖出,他的收益情况如何?
| 星期 | 一 | 二 | 三 | 四 | 五 |
| 每股涨跌 | +4 | +4.5 | -1 | -2.5 | -4 |
(2)本周内最高价是每股多少元?最低价是多少元?
(3)已知张智慧买进时付了0.15%的手续费,卖出时须付成交额0.15%的手续费和0.1%的交易税,如果张智慧在星期五收盘前将全部股票卖出,他的收益情况如何?
3. 在△ABC中,AB=AC,BD为△ABC的高,如果∠BAC=40°,则∠CBD的度数是( )
在△ABC中,AB=AC,BD为△ABC的高,如果∠BAC=40°,则∠CBD的度数是( )
 在△ABC中,AB=AC,BD为△ABC的高,如果∠BAC=40°,则∠CBD的度数是( )
在△ABC中,AB=AC,BD为△ABC的高,如果∠BAC=40°,则∠CBD的度数是( )| A. | 70° | B. | 40° | C. | 20° | D. | 30° |
4.甲、乙两班共有88人,若从甲班调3人到乙班,那么两班人数正好相等,设甲班原有人数是x人,可列出方程( )
| A. | 88-x=x-3 | B. | (88-x)+3=x-3 | C. | 88+x=x-3 | D. | (88-x)+3=x |
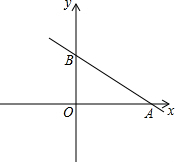 如图,在直角坐标系xOy中,O为坐标原点,直线y=kx-$\sqrt{3}$k+3交y轴正半轴于点B,交x轴于点A.
如图,在直角坐标系xOy中,O为坐标原点,直线y=kx-$\sqrt{3}$k+3交y轴正半轴于点B,交x轴于点A.