题目内容
16.如图1,在平面直角坐标系中,平行四边形ABCD在第一象限,且AB∥x 轴.直线y=-x从原点出发沿x轴正方向平移,被平行四边形ABCD截得的线段EF的长度y与平移的距离x的函数图象如图2所示,那么平行四边形ABCD的面积为12.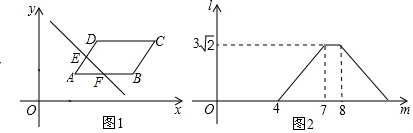
分析 根据图象可以得到当移动的距离是4时,直线经过点A,当移动距离是7时,直线经过D,在移动距离是8时经过B,则AB=8-4=4,当直线经过D点,则DF=3$\sqrt{2}$,作DM⊥AB于点M.利用三角函数即可求得DM即平行四边形的高,然后利用平行四边形的面积公式即可求解.
解答  解:根据图象可以得到当移动的距离是4时,直线经过点A,当移动距离是7时,直线经过D,在移动距离是8时经过B,
解:根据图象可以得到当移动的距离是4时,直线经过点A,当移动距离是7时,直线经过D,在移动距离是8时经过B,
则AB=8-4=4,
当直线经过D点,则DF=3$\sqrt{2}$,作DM⊥AB于点M.
∵y=-x与x轴形成的角是45°,
又∵AB∥x轴,
∴∠DFM=45°,
∴DM=DF•sin45°=3$\sqrt{2}$×$\frac{\sqrt{2}}{2}$=3,
则平行四边形的面积是:AB•DM=4×3=12,
故答案为:12.
点评 本题考查了函数的图象,根据图象理解AB的长度,正确求得平行四边形的高是关键.

练习册系列答案
 名校名师培优作业本加核心试卷系列答案
名校名师培优作业本加核心试卷系列答案 全程金卷系列答案
全程金卷系列答案
相关题目
11.在下列实数:-1.3,$\sqrt{2}$,0,2,-1中,绝对值最小的数是( )
| A. | -1.3 | B. | 0 | C. | $\sqrt{2}$ | D. | -1 |
5.化简:($\sqrt{x-3}$)2=( )
| A. | x-3 | B. | 3-x | C. | x+3 | D. | ±(x-3) |
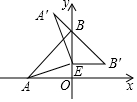 如图,在平面直角坐标系中,点A(-3,0)、点B(0,3),点E在OB上,将△ABE绕点E顺时针旋转90°得到△A′B′E,则A′B′的值为3$\sqrt{2}$.
如图,在平面直角坐标系中,点A(-3,0)、点B(0,3),点E在OB上,将△ABE绕点E顺时针旋转90°得到△A′B′E,则A′B′的值为3$\sqrt{2}$.