题目内容
3.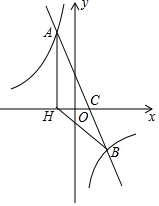 如图,在平面直角坐标系中,一次函数y=ax+b(a≠0)的图象与反比例函数y=$\frac{k}{x}$(k≠0)的图象交于A、B两点,与x轴交于点C,过点A作AH⊥x轴于点H,点O是线段CH的中点,AC=4$\sqrt{5}$,cos∠ACH=$\frac{\sqrt{5}}{5}$,点B的坐标为(4,n).
如图,在平面直角坐标系中,一次函数y=ax+b(a≠0)的图象与反比例函数y=$\frac{k}{x}$(k≠0)的图象交于A、B两点,与x轴交于点C,过点A作AH⊥x轴于点H,点O是线段CH的中点,AC=4$\sqrt{5}$,cos∠ACH=$\frac{\sqrt{5}}{5}$,点B的坐标为(4,n).(1)求该反比例函数和一次函数的解析式;
(2)求△BCH的面积.
分析 (1)首先利用锐角三角函数关系得出HC的长,再利用勾股定理得出AH的长,即可得出A点坐标,进而求出反比例函数解析式,再求出B点坐标,即可得出一次函数解析式;
(2)利用B点坐标的纵坐标再利用HC的长即可得出△BCH的面积.
解答 解:(1)∵AH⊥x轴于点H,AC=4$\sqrt{5}$,cos∠ACH=$\frac{\sqrt{5}}{5}$,
∴$\frac{HC}{AC}$=$\frac{\sqrt{5}}{5}$=$\frac{HC}{4\sqrt{5}}$,
解得:HC=4,
∵点O是线段CH的中点,
∴HO=CO=2,
∴AH=$\sqrt{A{C}^{2}-H{C}^{2}}$=8,
∴A(-2,8),
∴反比例函数解析式为:y=-$\frac{16}{x}$,
∴B(4,-4),
∴设一次函数解析式为:y=kx+b,
则$\left\{\begin{array}{l}{-2k+b=8}\\{4k+b=-4}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{k=-2}\\{b=4}\end{array}\right.$,
∴一次函数解析式为:y=-2x+4;
(2)由(1)得:△BCH的面积为:$\frac{1}{2}$×4×4=8.
点评 此题主要考查了反比例函数与一次函数解析式求法以及三角形面积求法,正确得出A点坐标是解题关键.

练习册系列答案
 能考试全能100分系列答案
能考试全能100分系列答案
相关题目
11.若x=-3,y=1,则代数式2x-3y+1的值为( )
| A. | -10 | B. | -8 | C. | 4 | D. | 10 |
8.下面四个几何体:

其中,俯视图是四边形的几何体个数是( )

其中,俯视图是四边形的几何体个数是( )
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
15.某班学生积极参加献爱心活动,该班50名学生的捐款统计情况如下表:
则他们捐款金额的中位数和平均数分别是( )
| 金额/元 | 5 | 10 | 20 | 50 | 100 |
| 人数 | 4 | 16 | 15 | 9 | 6 |
| A. | 10,20.6 | B. | 20,20.6 | C. | 10,30.6 | D. | 20,30.6 |
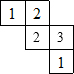 由一些大小相同的小正方体搭成的几何体的俯视图如图所示,其中正方形中的数字表示该位置上的小正方体的个数,那么该几何体的主视图是( )
由一些大小相同的小正方体搭成的几何体的俯视图如图所示,其中正方形中的数字表示该位置上的小正方体的个数,那么该几何体的主视图是( )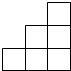

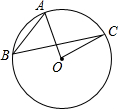 如图,OA、OC是⊙O的半径,点B在⊙O上,连接AB、BC,若∠ABC=40°,则∠AOC=80度.
如图,OA、OC是⊙O的半径,点B在⊙O上,连接AB、BC,若∠ABC=40°,则∠AOC=80度.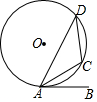 如图,$\widehat{AC}$=$\widehat{DC}$,AC平分∠DAB.
如图,$\widehat{AC}$=$\widehat{DC}$,AC平分∠DAB.