题目内容
 如图,AB,BC,CD分别与⊙O相切于E,F,G.且AB∥CD.BO=6cm,CO=8cm.
如图,AB,BC,CD分别与⊙O相切于E,F,G.且AB∥CD.BO=6cm,CO=8cm.(1)求证:BO⊥CO;
(2)求BE和CG的长.
考点:切线的性质,勾股定理,切线长定理,相似三角形的判定与性质
专题:几何图形问题
分析:(1)由AB∥CD得出∠ABC+∠BCD=180°,根据切线长定理得出OB、OC平分∠EBF和∠BCG,也就得出了∠OBC+∠OCB=
(∠ABC+∠DCB)=
×180°=90°.从而证得∠BOC是个直角,从而得出BO⊥CO;
(2)根据勾股定理求得AB=10cm,根据Rt△BOF∽Rt△BCO得出BF=3.6cm,根据切线长定理得出BE=BF=3.6cm,CG=CF,从而求得BE和CG的长.
| 1 |
| 2 |
| 1 |
| 2 |
(2)根据勾股定理求得AB=10cm,根据Rt△BOF∽Rt△BCO得出BF=3.6cm,根据切线长定理得出BE=BF=3.6cm,CG=CF,从而求得BE和CG的长.
解答:(1)证明:∵AB∥CD
∴∠ABC+∠BCD=180°
∵AB、BC、CD分别与⊙O相切于E、F、G,
∴BO平分∠ABC,CO平分∠DCB,
∴∠OBC=
∠ABC,∠OCB=
∠DCB,
∴∠OBC+∠OCB=
(∠ABC+∠DCB)=
×180°=90°,
∴∠BOC=90°,
∴BO⊥CO.
 (2)解:连接OF,则OF⊥BC,
(2)解:连接OF,则OF⊥BC,
∴Rt△BOF∽Rt△BCO,
∴
=
,
∵在Rt△BOC中,BO=6cm,CO=8cm,
∴BC=
=10cm,
∴
=
,
∴BF=3.6cm,
∵AB、BC、CD分别与⊙O相切,
∴BE=BF=3.6cm,CG=CF,
∵CF=BC-BF=10-3.6=6.4cm.
∴CG=CF=6.4cm.
∴∠ABC+∠BCD=180°
∵AB、BC、CD分别与⊙O相切于E、F、G,
∴BO平分∠ABC,CO平分∠DCB,
∴∠OBC=
| 1 |
| 2 |
| 1 |
| 2 |
∴∠OBC+∠OCB=
| 1 |
| 2 |
| 1 |
| 2 |
∴∠BOC=90°,
∴BO⊥CO.
 (2)解:连接OF,则OF⊥BC,
(2)解:连接OF,则OF⊥BC,∴Rt△BOF∽Rt△BCO,
∴
| BF |
| BO |
| BO |
| BC |
∵在Rt△BOC中,BO=6cm,CO=8cm,
∴BC=
| 62+82 |
∴
| BF |
| 6 |
| 6 |
| 10 |
∴BF=3.6cm,
∵AB、BC、CD分别与⊙O相切,
∴BE=BF=3.6cm,CG=CF,
∵CF=BC-BF=10-3.6=6.4cm.
∴CG=CF=6.4cm.
点评:本题主要考查了切线长定理、勾股定理、相似三角形的综合运用,正确理解切线长定理是解决本题的关键所在,虽然涉及的考点较多,但难度一般.

练习册系列答案
相关题目
下列各式正确的是( )
A、
| ||||
B、
| ||||
C、
| ||||
D、
|

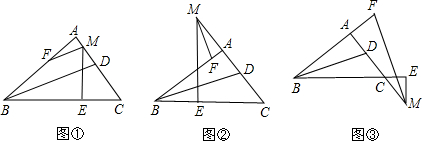
 已知:在△ABC中,∠BAC=90°,AB=AC,直线m经过点A,BD⊥直线m,CE⊥直线m,垂足分别为点D、E.证明:
已知:在△ABC中,∠BAC=90°,AB=AC,直线m经过点A,BD⊥直线m,CE⊥直线m,垂足分别为点D、E.证明: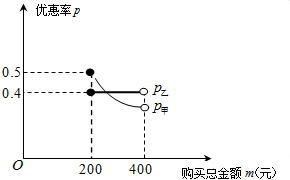 元旦期间,甲、乙两家商场都进行了促销活动,如何才能更好地衡量钏销对消费者受益程度的大小呢?某数学小组通过合作探究发现用优惠率p=
元旦期间,甲、乙两家商场都进行了促销活动,如何才能更好地衡量钏销对消费者受益程度的大小呢?某数学小组通过合作探究发现用优惠率p= 如图,在边长为1的正方形组成的网格中,△AOB的顶点均在格点上,点A、B的坐标分别是A(3,2)、B(1,3).求:
如图,在边长为1的正方形组成的网格中,△AOB的顶点均在格点上,点A、B的坐标分别是A(3,2)、B(1,3).求: