Question

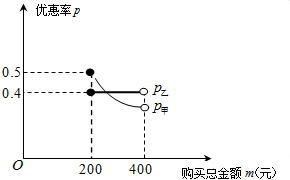元旦期间，甲、乙两家商场都进行了促销活动，如何才能更好地衡量钏销对消费者受益程度的大小呢？某数学小组通过合作探究发现用优惠率p=

k

m

（其中k代表优惠金额，m代表顾客购买商品的总金额）可以很好地进行衡量，优惠率p越大，消费者受益程度越大；反之就越小．经统计，若顾客在甲、乙两家商场购买商品的总金额都为m（200≤m＜400）元时，优惠率分别为p甲=

k甲

m

与p乙=

k乙

m

，它们与m的关系图象如图所示，其中其中p_甲与m成反比例函数关系，p_乙保持定值．
（1）求出k_甲的值，并用含m的代数式表示k_乙．
（2）当购买总金额m（元）在200≤m＜400的条件下时，指出甲、乙两家商场正在采取的促销方案分别是什么．
（3）品牌、质量、规格等都相同的基本种商品，在甲、乙两家商场的标价都是m（200≤m＜400）元，你认为选择哪家商场购买该商品花钱少些？请说明理由．

Answer 1

考点：反比例函数的应用,一次函数的应用

专题：

分析：（1）把m=200，p_甲=0.5代入p甲=

k甲

m

中求得得k_甲=100，然后根据p_乙始终为0.4，得到

k乙

m

=0.4，从而求得k_乙的值即可；
（2）当购买总金额都为m元，且在200≤m＜400的条件下时，代入可得甲家商场采取的促销方案是：优惠100元；乙家商场采取的促销方案是：打6折促销．
（3）根据当200≤m＜400时，甲家商场需花（m-100）元，乙家商场需花0.6m元．然后据m-100=0.6m，得m=250．即当m=250时，在两家商场购买花钱一样多．从而确定哪家更优惠．

解答：解：（1）把m=200，p_甲=0.5代入p甲=

k甲

m

中，
得k_甲=100．
由于p_乙始终为0.4，
即

k乙

m

=0.4，
∴k_乙=0.4m．
（2）由（1）及优惠率p的含义可知：
当购买总金额都为m元，且在200≤m＜400的条件下时，
甲家商场采取的促销方案是：优惠100元；
乙家商场采取的促销方案是：打6折促销．
（3）由上可知，当200≤m＜400时，甲家商场需花（m-100）元，乙家商场需花0.6m元．
据m-100=0.6m，得m=250．即当m=250时，在两家商场购买花钱一样多．
再由图象易知，当200≤m＜250时，甲商场更优惠；当250＜m＜400时，乙商场更优惠．

点评：本题考查了反比例函数的应用，解题的关键是从题目中整理出反比例函数模型，难度中等．