题目内容
12.先化简,再求值:$\frac{a}{a-b}$($\frac{1}{b}$-$\frac{1}{a}$)+$\frac{a-1}{b}$,其中a=2,b=$\frac{1}{3}$.分析 先对所求式子进行化简,然后根据a=2,b=$\frac{1}{3}$可以求得化简后式子的值,本题得以解决.
解答 解:$\frac{a}{a-b}$($\frac{1}{b}$-$\frac{1}{a}$)+$\frac{a-1}{b}$
=$\frac{a}{a-b}•\frac{a-b}{ab}+\frac{a-1}{b}$
=$\frac{1}{b}+\frac{a-1}{b}$
=$\frac{a}{b}$,
当a=2,b=$\frac{1}{3}$时,原式=$\frac{2}{\frac{1}{3}}=6$.
点评 本题考查分式的化简求值,解题的关键是会对所求的式子化简并求值.

练习册系列答案
相关题目
2. 如图,已知⊙O的半径为2,A为⊙O外一点,过点A作⊙O的一条切线AB,切点是B,AO的延长线交⊙O于点C,若∠BAC=30°,则劣弧$\widehat{BC}$的长为$\frac{4π}{3}$.
如图,已知⊙O的半径为2,A为⊙O外一点,过点A作⊙O的一条切线AB,切点是B,AO的延长线交⊙O于点C,若∠BAC=30°,则劣弧$\widehat{BC}$的长为$\frac{4π}{3}$.
 如图,已知⊙O的半径为2,A为⊙O外一点,过点A作⊙O的一条切线AB,切点是B,AO的延长线交⊙O于点C,若∠BAC=30°,则劣弧$\widehat{BC}$的长为$\frac{4π}{3}$.
如图,已知⊙O的半径为2,A为⊙O外一点,过点A作⊙O的一条切线AB,切点是B,AO的延长线交⊙O于点C,若∠BAC=30°,则劣弧$\widehat{BC}$的长为$\frac{4π}{3}$.
7.已知一组数据75,80,80,85,90,则它的众数和中位数分别为( )
| A. | 75,80 | B. | 80,85 | C. | 80,90 | D. | 80,80 |
12.已知∠1=37°36′,∠2=37.36°,则∠1与∠2的大小关系为( )
| A. | ∠1<∠2 | B. | ∠1=∠2 | C. | ∠1>∠2 | D. | 无法比较 |
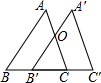 如图,△ABC中,BC=5cm,将△ABC沿BC方向平移至△A′B′C′的对应位置时,A′B′恰好经过AC的中点O,则△ABC平移的距离为2.5cm.
如图,△ABC中,BC=5cm,将△ABC沿BC方向平移至△A′B′C′的对应位置时,A′B′恰好经过AC的中点O,则△ABC平移的距离为2.5cm.