题目内容
5.操作发现:将一副直角三角板如图①摆放,能够发现等腰直角三角板ABC的斜边与含30°角的直角三角板DEF的长直角边DE重合.问题解决:将图①中的等腰直角三角板ABC绕点B顺时针旋转30°,点C落在BF上,AC与BD交于点O,连接CD,如图②.
(1)求证:AD∥BF;
(2)若AD=2,求AB的长.

分析 (1)作AM⊥BC,DN⊥BC,根据等腰直角三角形的性质得到AM=$\frac{1}{2}$BC,由于∠DBC=30°,得到DN=$\frac{1}{2}$BD,推出四边形AMND是矩形,根据矩形的性质即可得到结论;
(2)作AM⊥BC,DN⊥BC,设DF=a,解直角三角形得到NF=$\frac{1}{2}$a,DN=$\frac{\sqrt{3}}{2}$a,求得AM=DN=$\frac{\sqrt{3}}{2}$a,根据矩形的性质得到MN=AD=2,列方程即可得到结论.
解答 解:(1)如图2,作AM⊥BC,DN⊥BC, ∵△ABC是等腰直角三角形,
∵△ABC是等腰直角三角形,
∴AM=$\frac{1}{2}$BC,
∵∠DBC=30°,
∴DN=$\frac{1}{2}$BD,
∵BD=BC,
∴AM=DN,
∵AM⊥BC,DN⊥BC,
∴AM∥DN,
∴四边形AMND是矩形,
∴AD∥BC,
(2)如图2,作AM⊥BC,DN⊥BC,
设DF=a,
∵∠F=60°,
∴NF=$\frac{1}{2}$a,DN=$\frac{\sqrt{3}}{2}$a,
∴AM=DN=$\frac{\sqrt{3}}{2}$a,
∵BM=AM=$\frac{\sqrt{3}}{2}$a,
由(1)知四边形AMND是矩形,
∴MN=AD=2,
∵∠BDF=90°,
∴BF=2DF=2a,
∴BF=BM+MN+NF=$\frac{\sqrt{3}}{2}$a+2+$\frac{1}{2}$a=2a,
∴a=2-$\frac{2\sqrt{3}}{3}$,
∴BM=$\sqrt{3}$-1,
∴AB=$\sqrt{2}$BM=$\sqrt{6}$-$\sqrt{2}$.
点评 本题考查了旋转的性质,平行线的判定,等腰直角三角形的性质,矩形的判定和性质,特殊角的三角函数,正确的作出辅助线是解题的关键.

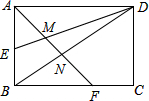 如图,矩形ABCD的边长AD=3,AB=2,E为AB的中点,F在边BC上,且BF=2FC,AF分别与DE、DB相交于点M,N,则MN的长为( )
如图,矩形ABCD的边长AD=3,AB=2,E为AB的中点,F在边BC上,且BF=2FC,AF分别与DE、DB相交于点M,N,则MN的长为( )| A. | $\frac{2\sqrt{2}}{5}$ | B. | $\frac{9\sqrt{2}}{20}$ | C. | $\frac{3\sqrt{2}}{4}$ | D. | $\frac{4\sqrt{2}}{5}$ |
| A. | 24cm2 | B. | 48cm2 | C. | 24πcm2 | D. | 12πcm2 |
| A. | 540° | B. | 720° | C. | 900° | D. | 360° |
| A. | 1,2,3 | B. | 2,3,4 | C. | 3,4,5 | D. | 4,5,6 |
 如图,在正十边形A1A2A3A4A5A6A7A8A9A10中,连接A1A4、A1A7,则∠A4A1A7=54°.
如图,在正十边形A1A2A3A4A5A6A7A8A9A10中,连接A1A4、A1A7,则∠A4A1A7=54°.