题目内容
17. 如图,AB是⊙O的切线,B为切点,AO与⊙O交于点C,若∠BAO=40°,则∠CBA的度数为( )
如图,AB是⊙O的切线,B为切点,AO与⊙O交于点C,若∠BAO=40°,则∠CBA的度数为( )| A. | 15° | B. | 20° | C. | 25° | D. | 30° |
分析 先利用切线的性质得∠ABO=90°,则利用互余得到∠O=50°,再根据等腰三角形的性质和三角形内角和定理可计算出∠OBC=65°,然后利用互余计算∠CBA的度数.
解答 解:∵AB是⊙O的切线,B为切点,
∴OB⊥BA,
∴∠ABO=90°,
∵∠BAO=40°,
∴∠O=50°,
∵OB=OC,
∴∠OBC=∠OCB=$\frac{1}{2}$(180°-50°)=65°,
∴∠CBA=90°-∠OBC=25°.
故选C.
点评 本题考查了切线的性质:圆的切线垂直于经过切点的半径.若出现圆的切线,必连过切点的半径,构造定理图,得出垂直关系.

练习册系列答案
相关题目
5.计算(2x-3)2等于( )
| A. | 2x2-6x+9 | B. | 2x2-12x+9 | C. | 4x2-6x+9 | D. | 4x2-12x+9 |
2.已知a<b,|a|=4,|b|=6,则a-b的值是( )
| A. | -2 | B. | -10 | C. | -2,-10或10 | D. | -2或-10 |
9.生物具有遗传多样性,遗传信息大多储存在DNA分子上,一个DNA分子直径约为0.000000201cm,这个数量用科学记数法可表示为( )
| A. | 0.201×10-6cm | B. | 2.01×10-6cm | C. | 0.201×10-7cm | D. | 2.01×10-7cm |
6.已知ab>15,且a=-5,则b的取值范围是 ( )
| A. | b>3 | B. | b<3 | C. | b>-3 | D. | b<-3 |
7.下列事件是随机事件的是( )
| A. | 画一个三角形其内角和为361° | |
| B. | 某种彩票中奖率是1%,则买这种彩票100张一定会中奖 | |
| C. | 任取一个实数,其相反数之和为0 | |
| D. | 外观相同的10件同种产品中有2件是不合格产品,现从中抽取一件恰为合格品 |
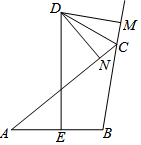 已知,如图,DE为△ABC的边AB的垂直平分线,CD为△ABC的外角平分线,与DE交于D,DM⊥BC于M,DN⊥AC于N,若CM=1,BC=3,求AN的长.
已知,如图,DE为△ABC的边AB的垂直平分线,CD为△ABC的外角平分线,与DE交于D,DM⊥BC于M,DN⊥AC于N,若CM=1,BC=3,求AN的长.