题目内容
 已知抛物线y=-x2+bx+c与x轴交于点A(-1,0)、B(3,0),与直线y=2x交于点C、D.
已知抛物线y=-x2+bx+c与x轴交于点A(-1,0)、B(3,0),与直线y=2x交于点C、D.(1)求抛物线的解析式和点C的坐标;
(2)将直线y=2x沿y轴向上平移,平移后的直线与抛物线交于点E、F(点E在点F的左侧),若EF=
| 5 |
(3)G、H为线段CD上关于点O对称的两点,且GH=2
| 5 |
考点:二次函数综合题
专题:
分析:(1)用等定系数法求得抛物线的解析式,再求出点C的坐标.
(2)先求出交点的坐标,利用两点间的距离公式求出b.
(3)先求出点H,G的坐标,再求出当平移2个单位时G,H正好与抛物线相交,再求出直线与抛物线只有一个交点时的k值,再求出k的范围.
(2)先求出交点的坐标,利用两点间的距离公式求出b.
(3)先求出点H,G的坐标,再求出当平移2个单位时G,H正好与抛物线相交,再求出直线与抛物线只有一个交点时的k值,再求出k的范围.
解答:解:(1)把A(-1,0)、B(3,0),代入y=-x2+bx+c得,
,解得,
∴抛物线的解析式为:y=-x2+2x+3,
∵与直线y=2x交于点C、D.
∴2x=-x2+2x+3,解得x=±
,
∴点C(
,2
),点D(-
,-2
).
(2)设平移后的直线解析式为:y=2x+b,
,解得
,
,
∴EF=
=2
,
∵EF=
,
∴2
=
,
∴b=
,
∵点E在点F的左侧,
∴E点的坐标为(-
,
).
(3)如图,

∵G、H为线段CD上关于点O对称的两点,GH=2
,
∴OH=
,
∵H在y=2x上,设H的坐标为(a,2a),
∴a2+(2a)2=5,
解得,a=±1,
∴H(1,2),G(-1,-2),
当抛物线y=-x2+2x+3,横坐标为-1时,y=0,横坐标为1时,y=4,
∴y=2x向上平移2个单位时G,H正好与抛物线相交,
∴此时k=2,
设平移后的直线解析式为:y=2x+k,
∵抛物线的解析式为:y=-x2+2x+3,
∴2x+k=-x2+2x+3,
化简x2=3-k
∴只有3-k>0,即k<3时直线y=2x+k与抛物线有两个交点,
综上所述只有当2≤k<3时,GH与抛物线有两个公共点.
|
|
∴抛物线的解析式为:y=-x2+2x+3,
∵与直线y=2x交于点C、D.
∴2x=-x2+2x+3,解得x=±
| 3 |
∴点C(
| 3 |
| 3 |
| 3 |
| 3 |
(2)设平移后的直线解析式为:y=2x+b,
|
|
|
∴EF=
(-2
|
| 3-b |
| 5 |
∵EF=
| 5 |
∴2
| 3-b |
| 5 |
| 5 |
∴b=
| 11 |
| 4 |
∵点E在点F的左侧,
∴E点的坐标为(-
| 1 |
| 2 |
| 7 |
| 4 |
(3)如图,

∵G、H为线段CD上关于点O对称的两点,GH=2
| 5 |
∴OH=
| 5 |
∵H在y=2x上,设H的坐标为(a,2a),
∴a2+(2a)2=5,
解得,a=±1,
∴H(1,2),G(-1,-2),
当抛物线y=-x2+2x+3,横坐标为-1时,y=0,横坐标为1时,y=4,
∴y=2x向上平移2个单位时G,H正好与抛物线相交,
∴此时k=2,
设平移后的直线解析式为:y=2x+k,
∵抛物线的解析式为:y=-x2+2x+3,
∴2x+k=-x2+2x+3,
化简x2=3-k
∴只有3-k>0,即k<3时直线y=2x+k与抛物线有两个交点,
综上所述只有当2≤k<3时,GH与抛物线有两个公共点.
点评:本题主要考查了二次函数的综合题,解题的关键是能得出在y=2x+k向上平移的过程中点G,H同时在抛物线上,此时k的值为2.

练习册系列答案
 星级口算天天练系列答案
星级口算天天练系列答案 芒果教辅达标测试卷系列答案
芒果教辅达标测试卷系列答案
相关题目
 如图,在正方形ABCD中,点E、F、G、H均在其内部,且DE=EF=FG=GH=HB=2,∠E=∠F=∠G=∠H=60°,则正方形ABCD的边长为( )
如图,在正方形ABCD中,点E、F、G、H均在其内部,且DE=EF=FG=GH=HB=2,∠E=∠F=∠G=∠H=60°,则正方形ABCD的边长为( ) 在一次蜡烛燃烧实验中,蜡烛燃烧时剩余部分的高度y(cm)与燃烧时间x(h)之间为一次函数关系.根据图象提供的信息,解答下列问题:
在一次蜡烛燃烧实验中,蜡烛燃烧时剩余部分的高度y(cm)与燃烧时间x(h)之间为一次函数关系.根据图象提供的信息,解答下列问题: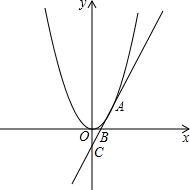 已知直线y1=2x-1分别交x轴、y轴于B、C,抛物线y2=mx2过直线y1=2x-1上点A(1,n).
已知直线y1=2x-1分别交x轴、y轴于B、C,抛物线y2=mx2过直线y1=2x-1上点A(1,n). 已知:如图,E,F是四边形ABCD的对角线AC上的两点,AF=CE,连接DE,DF,BE,BF.四边形DEBF为平行四边形.
已知:如图,E,F是四边形ABCD的对角线AC上的两点,AF=CE,连接DE,DF,BE,BF.四边形DEBF为平行四边形.