题目内容
解下列一元二次方程:
(1)2x2-5x-1=0(用配方法解);
(2)(2x-5)2=9(x+4)2.
(1)2x2-5x-1=0(用配方法解);
(2)(2x-5)2=9(x+4)2.
考点:解一元二次方程-因式分解法,解一元二次方程-配方法
专题:
分析:(1)根据配方法的步骤先两边都除以2,再移项,再配方,最后开方即可得出答案.
(2)先移项,然后利用平方差公式进行因式分解.
(2)先移项,然后利用平方差公式进行因式分解.
解答:(1)解:两边都除以2,得,x2-
x-
=0,
移项,得x2-
x=
,
配方,得x2-
x+
=
+
,
(x-
)2=
,
解这个方程,得x-
=±
,
则x1=
,x2=
.
(2)由原方程,得
(2x-5)2-9(x+4)2=0,
(2x-5+3x+12)(2x-5-3x-12)=0,
即:(5x+7)(-x-17)=0,
解得 x1=-17,x2=-
.
| 5 |
| 2 |
| 1 |
| 2 |
移项,得x2-
| 5 |
| 2 |
| 1 |
| 2 |
配方,得x2-
| 5 |
| 2 |
| 25 |
| 16 |
| 1 |
| 2 |
| 25 |
| 16 |
(x-
| 5 |
| 4 |
| 33 |
| 16 |
解这个方程,得x-
| 5 |
| 4 |
| ||
| 4 |
则x1=
5+
| ||
| 4 |
5-
| ||
| 4 |
(2)由原方程,得
(2x-5)2-9(x+4)2=0,
(2x-5+3x+12)(2x-5-3x-12)=0,
即:(5x+7)(-x-17)=0,
解得 x1=-17,x2=-
| 7 |
| 5 |
点评:本题考查了配方法解一元二次方程,关键是能正确配方,配方法的一般步骤:(1)把常数项移到等号的右边;(2)把二次项的系数化为1;(3)等式两边同时加上一次项系数一半的平方.

练习册系列答案
相关题目
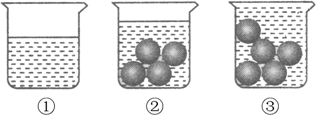
如图是测量一颗玻璃球体积的过程:
(1)将300mL的水倒进一个容量为500mL的杯子中;
(2)将四颗相同的玻璃球放入水中,结果水没有满;(3)再加一颗同样的玻璃球放入水中,结果水满溢出.
根据以上过程,推测这样一颗玻璃球的体积在(1mL水的体积为1cm3)( )
(1)将300mL的水倒进一个容量为500mL的杯子中;
(2)将四颗相同的玻璃球放入水中,结果水没有满;(3)再加一颗同样的玻璃球放入水中,结果水满溢出.
根据以上过程,推测这样一颗玻璃球的体积在(1mL水的体积为1cm3)( )

| A、20cm3以上,30cm3以下 |
| B、30cm3以上,40cm3以下 |
| C、40cm3以上,50cm3以下 |
| D、50cm3以上,60cm3以下 |
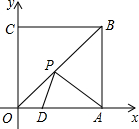 如图所示,四边形OABC为正方形,点A,C分别在x轴,y轴的正半轴上,点D在OA上,在OB上求作一点P,使得PD+PA的值最小,则可连接( )
如图所示,四边形OABC为正方形,点A,C分别在x轴,y轴的正半轴上,点D在OA上,在OB上求作一点P,使得PD+PA的值最小,则可连接( )| A、AC | B、BD | C、CD | D、不确定 |
 我们给出如下定义:点P是等边△ABC内一点,连结PA,PB,PC,我们称以PA,PB,PC为边构成的新三角形为原三角形的“联谊三角形”.
我们给出如下定义:点P是等边△ABC内一点,连结PA,PB,PC,我们称以PA,PB,PC为边构成的新三角形为原三角形的“联谊三角形”. 利用图14×4正方形网格,作出面积为5平方单位的正方形,并在图2数轴上作出
利用图14×4正方形网格,作出面积为5平方单位的正方形,并在图2数轴上作出