题目内容
利用图14×4正方形网格，作出面积为5平方单位的正方形，并在图2数轴上作出| 5 |
考点：勾股定理
专题：作图题
分析：已知图形是单位长度是1的网格，面积为5的正方形的边长为
，如果连接两个相邻的网格的对角线，则根据勾股定理得对角线长为
，依次连接两个相邻网格的对角线即得面积为5的正方形；过数轴上表示2的点C作数轴的垂线，然后以C为圆心，1个单位为半径画弧，交垂线于A点，连接OA，在Rt△OAC中，由OC=2，AC=1，利用勾股定理得到OA为
，故以O为圆心，OA长为半径画弧，与数轴交于点B，得到B为所求作的点．
| 5 |
| 5 |
| 5 |
解答：
解：如图1所示；
数轴上点B表示
对应的点（如图2所示）：
解：如图1所示；数轴上点B表示
| 5 |
点评：此题考查的知识点为勾股定理，关键是根据勾股定理得出如果连接两个相邻的网格的对角线，则根据勾股定理得对角线长为
．
| 5 |
练习册系列答案
相关题目
若a为无限不循环小数且a＞0，b是a的小数部分，则a-b是（ ）
| A、无理数 | B、整数 |
| C、有理数 | D、不能确定 |
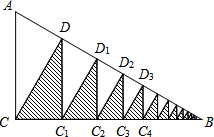如图，已知Rt△ABC中，∠B=30°，AC=2，作△CDB的高DC1，作△DC1B的高C1D1，…，就这样无限作下去，求图中阴影部分的面积．