题目内容
4.如果两个一次函数y=k1x+b1和y=k2x+b2满足k1=k2,b1≠b2,那么称这两个一次函数为“平行一次函数”.已知函数y=-2x+4的图象与x轴、y轴分别交于A、B两点,一次函数y=kx+b与y=-2x+4是“平行一次函数”
(1)若函数y=kx+b的图象过点(3,1),求b的值;
(2)若函数y=kx+b的图象与两坐标轴围成的面积是△AOB面积的$\frac{1}{4}$,求y=kx+b的解析式.
分析 (1)根据“平行一次函数”的定义即可得出k=-2,再由点(3,1)利用一次函数图象上点的坐标特征即可求出b值;
(2)分别令y=-2x+4中x=0、y=0求出与之对应的y、x值,即找出点A、B的坐标,利用三角形的面积公式求出S△AOB,同理找出函数y=kx+b的图象与两坐标轴围成的面积,根据两面积间的关系即可求出b值.
解答 解:(1)∵一次函数y=kx+b与y=-2x+4是“平行一次函数”,
∴k=-2,即y=-2x+b.
∵函数y=kx+b的图象过点(3,1),
∴1=-2×3+b,
∴b=7.
(2)在y=-2x+4中,令x=0,得y=4,令y=0,得x=2,
∴A(2,0),B(0,4),
∴S△AOB=$\frac{1}{2}$OA•OB=4.
由(1)知k=-2,则直线y=-2x+b与两坐标轴交点的坐标为($\frac{b}{2}$,0),(0,b),
于是有$\frac{1}{2}$|b|•|$\frac{b}{2}$|=4×$\frac{1}{4}$=1,
∴b=±2,
即y=kx+b的解析式为y=-2x+2或y=-2x-2.
点评 本题考查了两直线相交或平行问题、三角形的面积公式以及一次函数图象上点的坐标特征,解题的关键是:(1)根据点的坐标利用一次函数图象上点的坐标特征得出关于b的一元一次方程;(2)根据面积间的关系找出关于b的方程.本题属于基础题,难度不大,解决该题型题目时,根据三角形的面积公式结合面积间的关系找出方程是关键.

练习册系列答案
相关题目
15. 如图,OC平分∠AOB,OD平分∠AOC,∠AOD=35°,则∠AOB等于( )
如图,OC平分∠AOB,OD平分∠AOC,∠AOD=35°,则∠AOB等于( )
 如图,OC平分∠AOB,OD平分∠AOC,∠AOD=35°,则∠AOB等于( )
如图,OC平分∠AOB,OD平分∠AOC,∠AOD=35°,则∠AOB等于( )| A. | 80° | B. | 100° | C. | 110° | D. | 140° |
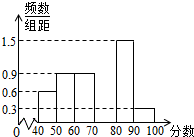 某校从参加计算机测试的学生中抽取了60名学生的成绩(40~100分)进行分析,并将其分成了六段后绘制成如图所示的频数分布直方图(其中70~80段因故看不清),若60分以上(含60分)为及格,试根据图中信息来估计这次测试的及格率约为75%.
某校从参加计算机测试的学生中抽取了60名学生的成绩(40~100分)进行分析,并将其分成了六段后绘制成如图所示的频数分布直方图(其中70~80段因故看不清),若60分以上(含60分)为及格,试根据图中信息来估计这次测试的及格率约为75%.