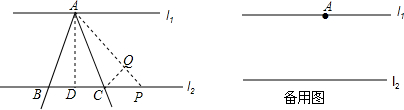题目内容
12．
如图：AB、CD、EF交于O点，AB⊥CD，OG平分∠AOE，∠COE=28°，求∠AOG的度数．
分析 先根据对顶角的性质求出∠COE的度数，进而可得出∠AOE的度数，根据角平分线的定义即可得出结论．
解答 解：∵AB⊥CD，
∴∠AOC=90°．
∵∠FOD与∠BOE是对顶角，
∴∠COE=∠FOD=28°，
∴∠BOE=90°-∠COE=62°，
∴∠AOE=180°-62°=118°，
∵OG平分∠AOE，
∴∠AOG=$\frac{1}{2}$∠AOE=$\frac{1}{2}$×118°=59°．
点评 本题考查的是垂线及角平分线的定义，熟知角平分线的定义是解答此题的关键．
练习册系列答案
相关题目
2．
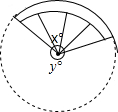如图，扇子的圆心角为x°，余下扇形的圆心角为y°，x与y的比通常按黄金比来设计，这样的扇子外形比较美观，若黄金比取0.6，则x为（ ）
如图，扇子的圆心角为x°，余下扇形的圆心角为y°，x与y的比通常按黄金比来设计，这样的扇子外形比较美观，若黄金比取0.6，则x为（ ）| A． | 144° | B． | 135° | C． | 136° | D． | 108° |
3．在Rt△ABC中，∠C=90°，sinB=$\frac{12}{13}$，则cosA的值为（ ）
| A． | $\frac{5}{12}$ | B． | $\frac{12}{5}$ | C． | $\frac{12}{13}$ | D． | $\frac{13}{12}$ |
20．以下叙述中错误的是（ ）
| A． | $±\sqrt{0.25}$=±0.5 | B． | $±\sqrt{0.25}$=0.5 | C． | 0的平方根是0 | D． | 1是1的平方根 |
如图，已知AD，BC相交于点O，OB=OD，∠ABD=∠CDB
