题目内容
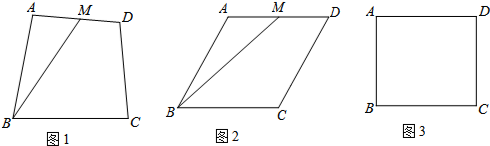
2.某课桌生产厂家研究发现,倾斜为12°-24°的桌面有利于学生保持躯体自然姿势.根据这一研究,厂家决定将水平桌面做成可调节角度的桌面.新桌面的设计图如图1所示,AB可绕点A旋转,在点C处安装一根长度一定且C处固定,可旋转的支撑臂CD,AC=30cm.(1)如图2中,当CD⊥AB于D时,测得∠BAC=24°,求此时支撑臂CD的长.
(2)在图3中,当CD不垂直AB时,测得∠BAC=12°,求此时AD的长(结果保留根号).[参考数据:sin24°=0.40,cos24°=0.91,tan24°=0.46,sin12°=0.20]

分析 (1)在Rt△ACD中利用锐角三角函数关系得出sin24°=$\frac{CD}{AC}$,代入数值计算即可求出CD的长;
(2)过点C作CE⊥AB于点E,在Rt△ACE中利用锐角三角函数关系得出sin12°=$\frac{CE}{AC}$,求出CE的长,再根据勾股定理求出DE,AE的长,进而得出AD的长.
解答 解:(1)在Rt△ACD中,∵∠DAC=24°,∠ADC=90°,
∴sin24°=$\frac{CD}{AC}$,
∴CD=AC•sin24°=30×0.40=12cm;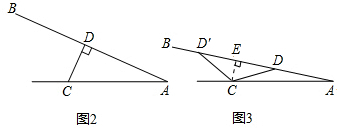 ∴此时支撑臂CD的长为12cm;
∴此时支撑臂CD的长为12cm;
(2)如图,过点C作CE⊥AB于点E,
当∠BAC=12°时,
∴sin12°=$\frac{CE}{AC}$=$\frac{CE}{30}$,
∴CE=30×0.20=6cm,
∵CD=12cm,
∴DE=$\sqrt{C{D}^{2}-C{E}^{2}}$=$\sqrt{1{2}^{2}-{6}^{2}}$=6$\sqrt{3}$cm,
∴AE=$\sqrt{3{0}^{2}-{6}^{2}}$=12$\sqrt{6}$cm,
∴AD的长为(12$\sqrt{6}$+6$\sqrt{3}$)cm或(12$\sqrt{6}$-6$\sqrt{3}$)cm.
点评 此题主要考查了解直角三角形的应用,锐角三角函数定义,勾股定理,准确作出辅助线构造直角三角形是解决第(2)小题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
13. 如图,在⊙O中,AC∥OB,∠BAO=25°,则∠BOC的度数为( )
如图,在⊙O中,AC∥OB,∠BAO=25°,则∠BOC的度数为( )
 如图,在⊙O中,AC∥OB,∠BAO=25°,则∠BOC的度数为( )
如图,在⊙O中,AC∥OB,∠BAO=25°,则∠BOC的度数为( )| A. | 80° | B. | 60° | C. | 50° | D. | 25° |
11.为了了解某小区居民的用水情况,随机抽查了该小区10户家庭的月用水量,结果如下:
(1)计算这家庭的平均月用水量;
(2)如果该小区有500户家庭,根据上面的计算结果,估计该小区居民每月共用水多少吨?
| 月用水量(吨) | 10 | 13 | 14 | 17 | 18 |
| 户数 | 2 | 2 | 3 | 2 | 1 |
(2)如果该小区有500户家庭,根据上面的计算结果,估计该小区居民每月共用水多少吨?
12.若平行四边形中两个内角的度数比为1:3,则其中较小的内角是( )
| A. | 30° | B. | 45° | C. | 60° | D. | 75° |
 如图:AB、CD、EF交于O点,AB⊥CD,OG平分∠AOE,∠COE=28°,求∠AOG的度数.
如图:AB、CD、EF交于O点,AB⊥CD,OG平分∠AOE,∠COE=28°,求∠AOG的度数.