题目内容
19.计算:(1)$\root{3}{-27}-\sqrt{0}-\sqrt{\frac{1}{16}}$
(2)$-{1^{2015}}-(1-0.5)÷(-\frac{3}{4})×[{4-{{(-4)}^2}}]$.
分析 (1)直接利用立方根、平方根的性质化简求出答案;
(2)直接利用有理数的乘方运算、有理数混合运算法则的性质化简求出答案.
解答 解:(1)$\root{3}{-27}-\sqrt{0}-\sqrt{\frac{1}{16}}$
=-3-0-$\frac{1}{4}$
=-3$\frac{1}{4}$;
(2)$-{1^{2015}}-(1-0.5)÷(-\frac{3}{4})×[{4-{{(-4)}^2}}]$
=-1+$\frac{1}{2}$×$\frac{4}{3}$×(4-16)
=-1+$\frac{1}{2}$×$\frac{4}{3}$×(-12)
=-9.
点评 此题主要考查了实数运算,正确根据相关知识化简各数是解题关键.

练习册系列答案
 数学奥赛暑假天天练南京大学出版社系列答案
数学奥赛暑假天天练南京大学出版社系列答案 南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案
南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案
相关题目
9.下列各式中,正确的是( )
| A. | x2y-2x2y=-x2y | B. | 2a+5b=5ab | C. | 7ab-3ab=4 | D. | a3+a2=a5 |
8.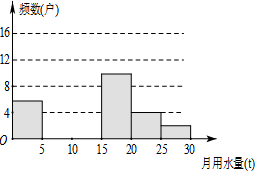 八(1)班同学为了解2015年某小区家庭月均用水情况,随机调查了该小区部分家庭,并将调查数据进行如下整理,
八(1)班同学为了解2015年某小区家庭月均用水情况,随机调查了该小区部分家庭,并将调查数据进行如下整理,
请解答以下问题:
(1)填空:m=12,n=0.08,并把频数分布直方图补充完整;
(2)若该小区有1000户家庭,求该小区月均用水量超过10t的家庭大约有多少户?
 八(1)班同学为了解2015年某小区家庭月均用水情况,随机调查了该小区部分家庭,并将调查数据进行如下整理,
八(1)班同学为了解2015年某小区家庭月均用水情况,随机调查了该小区部分家庭,并将调查数据进行如下整理,| 月均用水量x(t) | 频数(户) | 频率 |
| 0<x≤5 | 6 | 0.12 |
| 5<x≤10 | m | 0.24 |
| 10<x≤15 | 16 | 0.32 |
| 15<x≤20 | 10 | 0.20 |
| 20<x≤25 | 4 | n |
| 60≤x<70 | 2 | 0.04 |
(1)填空:m=12,n=0.08,并把频数分布直方图补充完整;
(2)若该小区有1000户家庭,求该小区月均用水量超过10t的家庭大约有多少户?
 如图,AB是⊙O的直径,C是⊙O上的一点,∠CAE=∠B,你认为AE与⊙O相切吗?为什么?
如图,AB是⊙O的直径,C是⊙O上的一点,∠CAE=∠B,你认为AE与⊙O相切吗?为什么? 如图,由若干个完全相同的小正方体堆成的一个几何体放置在平整的地面上.
如图,由若干个完全相同的小正方体堆成的一个几何体放置在平整的地面上. 如图,在△ABC中,D,E分别是AB,BC上的点,且DE∥AC,AE,CD交于点F,若S△BDE:S△DEC=1:3,则S△DEF:S△AFC=1:16.
如图,在△ABC中,D,E分别是AB,BC上的点,且DE∥AC,AE,CD交于点F,若S△BDE:S△DEC=1:3,则S△DEF:S△AFC=1:16.