题目内容
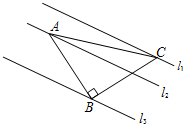 如图,已知△ABC中,∠ABC=90°,AB=BC,三角形的顶点在相互平行的三条直线l1,l2、l3上,且l1,l2之间的距离为1,l2、l3之间的距离为3,则AC的长是( )
如图,已知△ABC中,∠ABC=90°,AB=BC,三角形的顶点在相互平行的三条直线l1,l2、l3上,且l1,l2之间的距离为1,l2、l3之间的距离为3,则AC的长是( )A、2
| ||
B、5
| ||
C、2
| ||
| D、4 |
考点:全等三角形的判定与性质,勾股定理,等腰直角三角形
专题:
分析:过A、C点作l3的垂线构造出直角三角形,根据三角形全等求出BE=AD=3,由勾股定理求出BC的长,再利用勾股定理即可求出.
解答:解:作AD⊥l3于D,作CE⊥l3于E,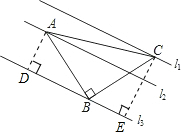
∵∠ABC=90°,
∴∠ABD+∠CBE=90°
又∠DAB+∠ABD=90°
∴∠BAD=∠CBE,
在△ABD和△BEC中,
,
∴△ABD≌△BCE(AAS),
∴BE=AD=3,
在Rt△BCE中,根据勾股定理,得BC=
=5,
在Rt△ABC中,根据勾股定理,得AC=
=
=5
.
故选B.

∵∠ABC=90°,
∴∠ABD+∠CBE=90°
又∠DAB+∠ABD=90°
∴∠BAD=∠CBE,
在△ABD和△BEC中,
|
∴△ABD≌△BCE(AAS),
∴BE=AD=3,
在Rt△BCE中,根据勾股定理,得BC=
| 32+(1+3)2 |
在Rt△ABC中,根据勾股定理,得AC=
| AB2+BC2 |
| 52+52 |
| 2 |
故选B.
点评:本题考查了全等三角形的性质和判定,勾股定理的应用,此题要作出平行线间的距离,构造直角三角形.运用全等三角形的判定和性质以及勾股定理进行计算.

练习册系列答案
 七彩题卡口算应用一点通系列答案
七彩题卡口算应用一点通系列答案
相关题目
 如图,已知Rt△ABC,以斜边AB为斜边作等腰Rt△ABD,连接CD,若AC=5,CD=
如图,已知Rt△ABC,以斜边AB为斜边作等腰Rt△ABD,连接CD,若AC=5,CD= 如图,在边长为1的正方形组成的网格中,△ABC的顶点都在格点上,将△ABC绕点C顺时针旋转60°,则顶点A所经过的路径长为
如图,在边长为1的正方形组成的网格中,△ABC的顶点都在格点上,将△ABC绕点C顺时针旋转60°,则顶点A所经过的路径长为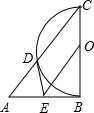 如图,以Rt△ABC的直角边BC为直径作半圆O交斜边于D,OE∥AC,交AB于E,连接DE.
如图,以Rt△ABC的直角边BC为直径作半圆O交斜边于D,OE∥AC,交AB于E,连接DE.