题目内容
已知方程2x+
-4=0的两个根为x1、x2.求
+
的值.
| 8x |
| 1 |
| x1-1 |
| 1 |
| x2-1 |
考点:根与系数的关系
专题:计算题
分析:原方程整理为x+
-2=0,利用换元法:设
=t,则t2+
t-2=0,设此方程的两根为a、b,根据根与系数的关系得到a+b=-
,ab=-2,利用x1=a2,x2=b2,计算出x1+x2=(a+b)2-2ab=6,x1x2=4,然后把原式通分后利用整体代入的方法计算.
| 2 |
| x |
| x |
| 2 |
| 2 |
解答:解:原方程整理为x+
-2=0,
设
=t,则t2+
t-2=0,设此方程的两根为a、b,则a+b=-
,ab=-2,
因为x1=a2,x2=b2,
所以x1+x2=(a+b)2-2ab=6,x1x2=4,
所以原式=
=
=
=-4.
| 2 |
| x |
设
| x |
| 2 |
| 2 |
因为x1=a2,x2=b2,
所以x1+x2=(a+b)2-2ab=6,x1x2=4,
所以原式=
| x1-1+x2-1 |
| (x1-1)(x2-1) |
| x1+x2-2 |
| x1x2-(x1+x2)+1 |
| 6-2 |
| 4-6+1 |
点评:本题考查了根与系数的关系:若x1,x2是一元二次方程ax2+bx+c=0(a≠0)的两根时,x1+x2=-
,x1x2=
.
| b |
| a |
| c |
| a |

练习册系列答案
相关题目
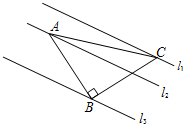 如图,已知△ABC中,∠ABC=90°,AB=BC,三角形的顶点在相互平行的三条直线l1,l2、l3上,且l1,l2之间的距离为1,l2、l3之间的距离为3,则AC的长是( )
如图,已知△ABC中,∠ABC=90°,AB=BC,三角形的顶点在相互平行的三条直线l1,l2、l3上,且l1,l2之间的距离为1,l2、l3之间的距离为3,则AC的长是( )A、2
| ||
B、5
| ||
C、2
| ||
| D、4 |
弦心距为4,弦长为8的弦所对的劣弧长是( )
| A、8π | ||
| B、4π | ||
C、
| ||
D、2
|
某抗震蓬的顶部是圆锥形,这个圆锥的底面直径为10米,母线长为6米,为了防雨,需要在它的顶部铺上油毡,所需油毡的面积至少是( )
| A、30л米2 |
| B、55л米2 |
| C、30米2 |
| D、60л米2 |
 如图,M,N为线段AB上的两个三等分点,点A,B在圆O上,求证:∠OMN=∠ONM.
如图,M,N为线段AB上的两个三等分点,点A,B在圆O上,求证:∠OMN=∠ONM.