Question

7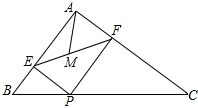．如图，在△ABC中，AB=3，AC=4，BC=5，P为边BC上一动点，PE⊥AB于E，PF⊥AC于F，M为EF中点，则AM的最小值为$\frac{6}{5}$．

Answer 1

分析 先根据矩形的判定得出AEPF是矩形，再根据矩形的性质得出EF，AP互相平分，且EF=AP，再根据垂线段最短的性质就可以得出AP⊥BC时，AP的值最小，即AM的值最小，根据面积关系建立等式求出其解即可．

解答 解：∵AB=3，AC=4，BC=5，
∴∠EAF=90°，
∵PE⊥AB于E，PF⊥AC于F，
∴四边形AEPF是矩形，
∴EF，AP互相平分．且EF=AP，
∴EF，AP的交点就是M点．
∵当AP的值最小时，AM的值就最小，
∴当AP⊥BC时，AP的值最小，即AM的值最小．
∵$\frac{1}{2}$AP．BC=$\frac{1}{2}$AB．AC，
∴AP．BC=AB．AC．
∵AB=3，AC=4，BC=5，
∴5AP=3×4，
∴AP=$\frac{12}{5}$，
∴AM=$\frac{6}{5}$；
故答案为：$\frac{6}{5}$．

点评 本题考查了矩形的性质的运用，勾股定理的运用，三角形的面积公式的运用，垂线段最短的性质的运用，解答时求出AP的最小值是关键．