题目内容
19.已知a、b、c是△ABC的三边的长,(1)若满足(a-b)b-(b-a)c=0,试判断此三角形的形状.
(2)若满足a2+2b2+c2-2b(a+c)=0,试判断此三角形的形状.
分析 把所给的等式能进行因式分解的要因式分解,整理为非负数相加得0的形式,求出三角形三边的关系,进而判断三角形的形状.
解答 解:(1)∵(a-b)b-(b-a)c=0,
∴(a-b)(b+c)=0,
∵a、b、c是△ABC的三边的长,
∴b+c≠0,
∴a-b=0,
∴a=b,
∴△ABC是等腰三角形;
(2)∵a2+2b2+c2-2b(a+c)=0,
∴(a-b)2+(b-c)2=0,
∴a=b,b=c,
∴a=b=c,
∴△ABC是等边三角形.
点评 本题考查了三角形的形状判定,非负数的性质,根据几个非负数的和等于0,则每一个算式都等于0列式是解题的关键.

练习册系列答案
相关题目
4.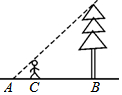 如图,身高1.6m的某学生想测量一棵大树的高度,她沿着树影BA由B向A走去,当走到C点时,她的影子顶端正好与树的影子顶端重合,测得BC=3.2m,CA=0.8m,则树的高度为( )
如图,身高1.6m的某学生想测量一棵大树的高度,她沿着树影BA由B向A走去,当走到C点时,她的影子顶端正好与树的影子顶端重合,测得BC=3.2m,CA=0.8m,则树的高度为( )
 如图,身高1.6m的某学生想测量一棵大树的高度,她沿着树影BA由B向A走去,当走到C点时,她的影子顶端正好与树的影子顶端重合,测得BC=3.2m,CA=0.8m,则树的高度为( )
如图,身高1.6m的某学生想测量一棵大树的高度,她沿着树影BA由B向A走去,当走到C点时,她的影子顶端正好与树的影子顶端重合,测得BC=3.2m,CA=0.8m,则树的高度为( )| A. | 4.8 m | B. | 6.4 m | C. | 8 m | D. | 10 m |
 如图,在?ABCD中,对角线AC与BD相交于点O,BD⊥AD,AB=10,AD=8.求OB的长度及?ABCD的面积.
如图,在?ABCD中,对角线AC与BD相交于点O,BD⊥AD,AB=10,AD=8.求OB的长度及?ABCD的面积.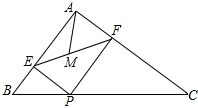 如图,在△ABC中,AB=3,AC=4,BC=5,P为边BC上一动点,PE⊥AB于E,PF⊥AC于F,M为EF中点,则AM的最小值为$\frac{6}{5}$.
如图,在△ABC中,AB=3,AC=4,BC=5,P为边BC上一动点,PE⊥AB于E,PF⊥AC于F,M为EF中点,则AM的最小值为$\frac{6}{5}$.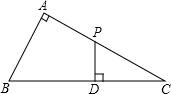 如图,在△ABC中,∠A=90°,P为AC的中点,PD⊥BC,D为垂足,求证:BD2-CD2=AB2.
如图,在△ABC中,∠A=90°,P为AC的中点,PD⊥BC,D为垂足,求证:BD2-CD2=AB2.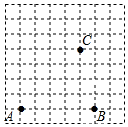 画图并回答:
画图并回答: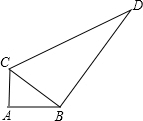 一块试验田的形状如图所示,∠A=90°,AC=3m,AB=4m,BD=12m,CD=13m,求这块试验田的面积.
一块试验田的形状如图所示,∠A=90°,AC=3m,AB=4m,BD=12m,CD=13m,求这块试验田的面积.