题目内容
19.某校运动会需购买A、B两种奖品,若购买A种奖品3件和B种奖品2件,共需60元;若购买A种奖品5件和B种奖品3件,共需95元.(1)求A、B两种奖品的单价各是多少元?
(2)学校计划购买A、B两种奖品共100件,且A种奖品的数量不大于B种奖品数量的3倍,设购买A种奖品m件,购买费用为W元,写出W(元)与m(件)之间的函数关系式.并求怎样购买使费用最少,最少费用是多少元?
分析 (1)设A奖品的单价是x元,B奖品的单价是y元,根据条件建立方程组求出其解即可;
(2)根据总费用=两种奖品的费用之和表示出W与m的关系式,并有条件建立不等式组求出x的取值范围,由一次函数的性质就可以求出结论.
解答 解(1)设A奖品的单价是x元,B奖品的单价是y元,由题意,得
$\left\{\begin{array}{l}{3x+2y=60}\\{5x+3y=95}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{x=10}\\{y=15}\end{array}\right.$.
答:A奖品的单价是10元,B奖品的单价是15元;
(2)由题意,得
W=10m+15(100-m)=-5m+1500
∴m≤3(100-m),
解得:m≤75,
∵W=-5m+1500,
∴k=-5<0,
∴W随m的增大而减小,
∴m=75时,W最小=1125,
∴应买A种奖品75件,B种奖品25件,才能使总费用最少为1125元.
点评 本题考查了一次函数的性质的运用,二元一次方程组的运用,一元一次不等式组的运用,解答时求一次函数的解析式是关键.

练习册系列答案
相关题目
14.将直线y=3x-2平移后,得到直线y=3x+6,则原直线( )
| A. | 沿y轴向上平移了8个单位 | B. | 沿y轴向下平移了8个单位 | ||
| C. | 沿x轴向左平移了8个单位 | D. | 沿x轴向右平移了8个单位 |
4.甲乙两地相距100千米,一艘轮船往返两地,顺流用4小时,逆流用5小时,那么这艘轮船在静水中的船速与水流速度分别是( )
| A. | 24km/h,8km/h | B. | 22.5km/h,2.5km/h | ||
| C. | 18km/h,24km/h | D. | 12.5km/h,1.5km/h |

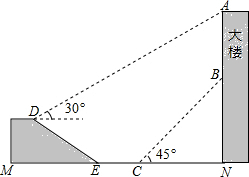 如图,大楼AN上悬挂一条幅AB,小颖在坡面D处测得条幅顶部A的仰角为30°,沿坡面向下走到坡脚E处,然后向大楼方向继续行走10米来到C处,测得条幅的底部B的仰角为45°,此时小颖距大楼底端N处20米.已知坡面DE=20米,山坡的坡度i=1:$\sqrt{3}$(即tan∠DEM=1:$\sqrt{3}$),且D、M、E、C、N、B、A在同一平面内,E、C、N在同一条直线上,求条幅的长度(结果精确到1米)(参考数据:$\sqrt{3}$≈1.73,$\sqrt{2}$≈1.41)
如图,大楼AN上悬挂一条幅AB,小颖在坡面D处测得条幅顶部A的仰角为30°,沿坡面向下走到坡脚E处,然后向大楼方向继续行走10米来到C处,测得条幅的底部B的仰角为45°,此时小颖距大楼底端N处20米.已知坡面DE=20米,山坡的坡度i=1:$\sqrt{3}$(即tan∠DEM=1:$\sqrt{3}$),且D、M、E、C、N、B、A在同一平面内,E、C、N在同一条直线上,求条幅的长度(结果精确到1米)(参考数据:$\sqrt{3}$≈1.73,$\sqrt{2}$≈1.41)