题目内容
8.在《九章算术》中记载了一道有趣的数学题:“今有池方一丈,葭生其中央,出水一尺,引葭赴岸,适与岸齐,问水深,葭长各几何?”这道题的意思是说:有一个边长为一丈的正方形水池,在池的正中央长着一根芦苇,芦苇露出水面一尺,若将芦苇拉到池边中点处,芦苇的顶端恰好与水面齐平,问水有多深?,芦苇有多长(1丈=10尺)?请你解决这个问题.分析 找到题中的直角三角形,设水深为x尺,根据勾股定理可得x2+($\frac{10}{2}$)2=(x+1)2,再解答即可.
解答 解;设水深为x尺,则芦苇长为(x+1)尺,
根据勾股定理得:x2+($\frac{10}{2}$)2=(x+1)2,
解得:x=12,
芦苇的长度=x+1=12+1=13(尺),
答:水池深12尺,芦苇长13尺.
点评 此题主要考查了勾股定理得应用,关键是从题中抽象出勾股定理这一数学模型,画出准确的示意图.领会数形结合的思想的应用.

练习册系列答案
相关题目
20.若a>b,则下列不等式一定成立的是( )
| A. | a-b<0 | B. | $\frac{a}{3}$<$\frac{b}{3}$ | C. | -a>-b | D. | -a+1<-b+1 |
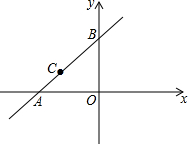 如图,直线y=x+4与坐标轴交于点A、B,点C(-3,m)在直线AB上,在y轴上找一点P,使PA+PC的值最小,求这个最小值及点P的坐标.
如图,直线y=x+4与坐标轴交于点A、B,点C(-3,m)在直线AB上,在y轴上找一点P,使PA+PC的值最小,求这个最小值及点P的坐标.