题目内容
2.先化筒,再求代数式$\frac{4{y}^{2}-{x}^{2}}{-{x}^{2}-4{y}^{2}+4xy}$的值,其中x=$\frac{5}{4}$,y=$-\frac{1}{2}$.分析 分子、分母因式分解约分,然后代入计算即可.
解答 解:原式=$\frac{(2y-x)(2y+x)}{-(2y-x)^{2}}$=$\frac{x+2y}{x-2y}$,
当x=$\frac{5}{4}$,y=-$\frac{1}{2}$时,原式=$\frac{\frac{5}{4}-1}{\frac{5}{4}+1}$=$\frac{1}{9}$.
点评 本题考查分式的化简求值,解题的关键是熟练掌握因式分解,记住分子分母因式分解后约分,代入计算时不要粗心大意,属于中考常考题型.

练习册系列答案
相关题目
12.在直角坐标系中,点M($\sqrt{3}$,-2)在( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
12.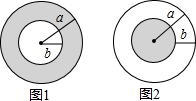 如图1,在一个半径为a的大圆内,挖去一个半径为b(0<b<a)的小圆,剩下部分(阴影部分)的面积为S1;如图2,在一个半径为a的大圆上剪去一个圆环(内径为b),剩下部分(阴影部分)的面积为S2,则S1与S2的大小关系是( )
如图1,在一个半径为a的大圆内,挖去一个半径为b(0<b<a)的小圆,剩下部分(阴影部分)的面积为S1;如图2,在一个半径为a的大圆上剪去一个圆环(内径为b),剩下部分(阴影部分)的面积为S2,则S1与S2的大小关系是( )
 如图1,在一个半径为a的大圆内,挖去一个半径为b(0<b<a)的小圆,剩下部分(阴影部分)的面积为S1;如图2,在一个半径为a的大圆上剪去一个圆环(内径为b),剩下部分(阴影部分)的面积为S2,则S1与S2的大小关系是( )
如图1,在一个半径为a的大圆内,挖去一个半径为b(0<b<a)的小圆,剩下部分(阴影部分)的面积为S1;如图2,在一个半径为a的大圆上剪去一个圆环(内径为b),剩下部分(阴影部分)的面积为S2,则S1与S2的大小关系是( )| A. | S1>S2 | B. | S1≥S2 | C. | S1<S2 | D. | S1≤S2 |
10.下列运算正确的是( )
| A. | x3•x2=x6 | B. | (ab)2=ab2 | C. | a6+a6=a12 | D. | b2+b2=2b2 |
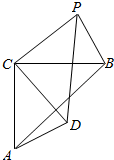 如图,等腰直角△ABC,AC=BC=$\sqrt{5}$,等腰直角△CDP中,CD=CP,且PB=$\sqrt{2}$,将△CDP绕点C旋转.
如图,等腰直角△ABC,AC=BC=$\sqrt{5}$,等腰直角△CDP中,CD=CP,且PB=$\sqrt{2}$,将△CDP绕点C旋转.