题目内容
若x2+x-2=0,则x3+2x2-x+2012的值是 .
考点:因式分解的应用
专题:
分析:x2+x-2=0变形得x2+x=2,把原式适当变形,整体代入求得答案即可.
解答:解:∵x2+x-2=0,
∴x2+x=2,
∴x3+2x2-x+2012
=x(x2+x)+x2-x+2012
=2x+x2-x+2012
=x2+x+2012
=2+2012
=2014.
故答案为:2014.
∴x2+x=2,
∴x3+2x2-x+2012
=x(x2+x)+x2-x+2012
=2x+x2-x+2012
=x2+x+2012
=2+2012
=2014.
故答案为:2014.
点评:本题主要考查了整体思想在因式分解中的灵活运用,注意分组分解和整体代入思想的渗透.

练习册系列答案
 浙大优学小学年级衔接捷径浙江大学出版社系列答案
浙大优学小学年级衔接捷径浙江大学出版社系列答案
相关题目
下列说法正确的是( )
| A、数据1,2,3,2,5的中位数是3 |
| B、数据5,5,7,5,7,6,11的众数是7 |
| C、若甲组数据方差S2甲=0.15,乙组数据方差S2乙=0.15,则乙组数据比甲组数据稳定 |
| D、数据1,2,2,3,7的平均数是3 |
某工厂加强节能措施,去年下半年与上半年相比,月平均用电量减少2000度,全年用电量15万度.如果设上半年每月平均用电x度,则所列方程正确的是( )
| A、6x+6(x-2000)=150000 |
| B、6x+6(x+2000)=150000 |
| C、6x+6(x-2000)=15 |
| D、6x+6(x+2000)=15 |
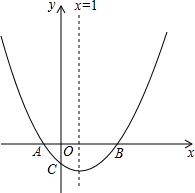 如图,抛物线y=
如图,抛物线y= 如图所示,是由若干个小立方块搭成的几何体,分别画出从正面,上面,左面看到它的形状图,并在小正方形内填上表示小立方块的个数.
如图所示,是由若干个小立方块搭成的几何体,分别画出从正面,上面,左面看到它的形状图,并在小正方形内填上表示小立方块的个数. 如图,⊙O的半径为1,弦AB、CD互相垂直,垂足为E,求AE2+BE2+CE2+DE2的值.
如图,⊙O的半径为1,弦AB、CD互相垂直,垂足为E,求AE2+BE2+CE2+DE2的值.