Question

18．在△ABC中，∠BAC=90°，AB=AC，∠ABC=∠ACB=45°，在△ABC外侧作∠ACM，使得∠ACM=$\frac{1}{2}$∠ABC，点D是射线CB上的动点，过点D作直线CM的垂线，垂足为E，交直线AC于F．
（1）当点D与点B重合时，如图1所示，线段DF与EC的数量关系是DF=2EC；
（2）当点D运动到CB延长线上某一点时，线段DF和EC是否保持上述数量关系？请在图2中画出图形，并说明理由．

Answer 1

分析 （1）如图1，延长BA、CM交于点N，先证明BC=BN，得出CN=2CE，再证明△BAF≌△CAN，得对应边相等BF=CN，即可得出结论；
（2）如图2，结论仍然成立，作∠PDE=22.5，交CE的延长线于P点，交CA的延长线于N，先证明DC=PD，得出PC=2CE，再证明∴△DNF≌△PNC，得对应边相等DF=PC，即可得出结论．

解答 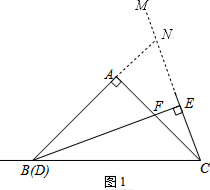解：（1）如图1，DF=2EC，理由是：
延长BA、CM交于点N，
∵∠BAC=∠BEC=90°，∠AFB=∠EFC，
∴∠ABE=∠ACM=$\frac{1}{2}$∠ABC，
∴BE平分∠ABC，
∵BE⊥CN，
∴BC=BN，
∴E是CN的中点，
∴NC=2CE，
∵AB=AC，∠BAC=∠CAN=90°，
∴△BAF≌△CAN，
∴BF=CN，
∴BF=2EC，即DF=2EC；
（2）仍然成立，DF=2EC；
理由如下：如图2，作∠PDE=22.5，交CE的延长线于P点，交CA的延长线于N，
∵DE⊥PC，∠ECD=67.5，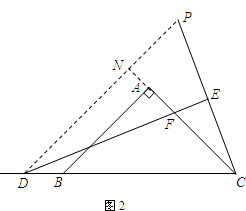
∴∠EDC=22.5°，
∴∠PDE=∠EDC，∠NDC=45°，
∴∠DPC=67.5°，
在△DPE和△DEC中，$\left\{\begin{array}{l}∠PDE=∠CDE\\∠DPE=∠DCE\\ DE=DE\end{array}\right.$，

∴△DPE≌△DEC（AAS），
∴PD=CD，PE=EC，
∴PC=2CE，
∵∠NDC=45°，∠NCD=45°，
∴∠NCD=∠NDC，∠DNC=90°，
∴△NDC是等腰直角三角形
∴ND=NC且∠DNC=∠PNC，
在△DNF和△PNC中，$\left\{\begin{array}{l}∠DNC=∠PNC\\ ND=NC\\∠PDE=∠PCN\end{array}\right.$，
∴△DNF≌△PNC（ASA），
∴DF=PC，
∴DF=2CE．

点评 本题考查了全等三角形、等腰直角三角形的性质和判定，恰当地做出辅助线，构建全等三角形是本题的关键；巧妙地运用了∠ACM=$\frac{1}{2}$∠ABC，为证两三角形全等创造条件．