题目内容
6．顺次连接对角线互相垂直的四边形的中点的四边形是（ ）| A． | 矩形 | B． | 直角梯形 | C． | 菱形 | D． | 正方形 |
分析 根据四边形对角线互相垂直，运用三角形中位线平行于第三边证明四个角都是直角，判断是矩形．
解答 解：如图：∵E、F、G、H分别为各边中点，
∴EF∥GH∥DB，EF=GH=$\frac{1}{2}$DB，
EH=FG=$\frac{1}{2}$AC，EH∥FG∥AC，
∵DB⊥AC，
∴EF⊥EH，
∴四边形EFGH是矩形．
故选：A．
点评 本题考查的是三角形中位线定理，掌握三角形的中位线平行于第三边且等于第三边的一半是解题的关键．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
16．
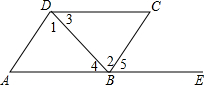如图，点A，B，E在一条直线上，下列条件中不能判断AD∥BC的是（ ）
如图，点A，B，E在一条直线上，下列条件中不能判断AD∥BC的是（ ）| A． | ∠1=∠2 | B． | ∠3=∠4 | C． | ∠A=∠5 | D． | ∠A+∠ABC=180° |
17．
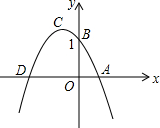如图是二次函数y=mx2+nx+b的图象，已知它的顶点C在第二象限，且经过点A（1，0），点B（0，1），与x轴另一交点为D，当△ACD的面积为△ABD面积的$\frac{3}{2}$倍时，m的值为（ ）
如图是二次函数y=mx2+nx+b的图象，已知它的顶点C在第二象限，且经过点A（1，0），点B（0，1），与x轴另一交点为D，当△ACD的面积为△ABD面积的$\frac{3}{2}$倍时，m的值为（ ）| A． | $\sqrt{3}$-2 | B． | -2±$\sqrt{3}$ | C． | 2-$\sqrt{3}$ | D． | -2-$\sqrt{3}$ |
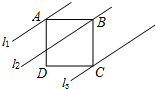如图，已知正方形ABCD，直线l1、l2、l3分别通过A、B、C三点，且l1∥l2∥l3，若l1与l2的距离为3，l2与l3的距离为5，则正方形ABCD的面积等于（ ）
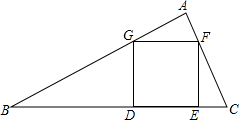已知，如图所示，在△ABC中，正方形DEFG的顶点D，E在边BC上，另两个顶点G，F分别在边AB，AC上，且S△AGF=S△CEF=1，S△BDG=3，求S正方形DEFG．