题目内容
11.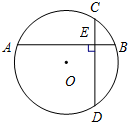 如图,两条互相垂直的弦将⊙O分成四部分,相对的两部分面积之和分别记为S1、S2,若圆心O到两弦的距离分别为4和6,则|S1-S2|=96.
如图,两条互相垂直的弦将⊙O分成四部分,相对的两部分面积之和分别记为S1、S2,若圆心O到两弦的距离分别为4和6,则|S1-S2|=96.
分析 作关于O的对称弦,得出两面积之差=长方形的面积,求出长方形的面积即可.
解答  解:如图,作弦AB、CD关于O的对称弦,
解:如图,作弦AB、CD关于O的对称弦,
根据图形可知阴影部分的面积减去空白部分的面积正好是中间的长方形的面积,
∵圆心到两弦的距离分别为4和6,
∴长方形的长是6+6=12,宽是4+4=8,面积为12×8=96,
即|S1-S2|=96,
故答案为:96.
点评 本题考查了中心对称,长方形的性质,垂径定理的应用,题目比较好,但是有一定的难度.

练习册系列答案
相关题目
6.在同一直角坐标系中,P、Q分别是y=-x+3与y=3x-5的图象上的点,且P、Q关于x轴对称,则点P的坐标是( )
| A. | (-$\frac{1}{2}$,$\frac{7}{2}$) | B. | (-2,5) | C. | (1,2) | D. | (-4,7) |
1.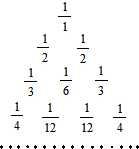 如图所示的数阵叫“莱布尼兹调和三角形”,它们是由整数的倒数组成的,第n行有n个数,且两端的数均为$\frac{1}{n}$,每个数是它下一行左右相邻两数的和,则第8行第2个数(从左到右)为( )
如图所示的数阵叫“莱布尼兹调和三角形”,它们是由整数的倒数组成的,第n行有n个数,且两端的数均为$\frac{1}{n}$,每个数是它下一行左右相邻两数的和,则第8行第2个数(从左到右)为( )
 如图所示的数阵叫“莱布尼兹调和三角形”,它们是由整数的倒数组成的,第n行有n个数,且两端的数均为$\frac{1}{n}$,每个数是它下一行左右相邻两数的和,则第8行第2个数(从左到右)为( )
如图所示的数阵叫“莱布尼兹调和三角形”,它们是由整数的倒数组成的,第n行有n个数,且两端的数均为$\frac{1}{n}$,每个数是它下一行左右相邻两数的和,则第8行第2个数(从左到右)为( )| A. | $\frac{1}{56}$ | B. | $\frac{1}{60}$ | C. | $\frac{1}{64}$ | D. | $\frac{1}{168}$ |
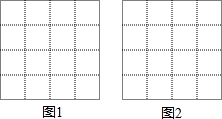 如图,正方形网格中的每个小正方形边长都为1,每个小正方形的顶点叫格点,以格点为顶点分别按下列要求画图:
如图,正方形网格中的每个小正方形边长都为1,每个小正方形的顶点叫格点,以格点为顶点分别按下列要求画图: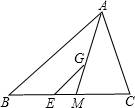 如图,点G为△ABC的重心,GE∥AB,求$\frac{BE}{CE}$的值.
如图,点G为△ABC的重心,GE∥AB,求$\frac{BE}{CE}$的值.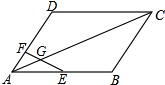 如图,在?ABCD中,E为AB的中点,点F在AD上,EF交AC于点G,AF=2,DF=4,AG=3,求AC的长.
如图,在?ABCD中,E为AB的中点,点F在AD上,EF交AC于点G,AF=2,DF=4,AG=3,求AC的长.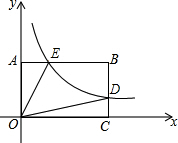 如图,反比例函数y=$\frac{k}{x}$(k>0)图象过矩形OABC边BC中点D交AB于点E,四边形ODBE的面积为2,则结论:①S△OAE=S△OCD;②E为AB中点;③k=2;④AO=AE,其中正确的序号为①②③.
如图,反比例函数y=$\frac{k}{x}$(k>0)图象过矩形OABC边BC中点D交AB于点E,四边形ODBE的面积为2,则结论:①S△OAE=S△OCD;②E为AB中点;③k=2;④AO=AE,其中正确的序号为①②③.