题目内容
二次函数y=x2-4x-3的顶点坐标是_____________.
 (2,﹣7)
【解析】试题分析:原式化为顶点式解析式,即为y=(x-2)2-7,所以其顶点坐标是(2,﹣7).
(2,﹣7)
【解析】试题分析:原式化为顶点式解析式,即为y=(x-2)2-7,所以其顶点坐标是(2,﹣7).
已知一直角边和这条直角边的对角,求作直角三角形(用尺规作图,不写作法,但要保留作图痕迹).
 见解析
【解析】试题分析:根据题意写出已知和求作,然后再画出图形即可.
试题解析:已知:线段a和∠α,如下图(1).
求作:Rt△ABC,使BC=a,∠C=90?,∠A=∠α.
作法:(1)作∠α的余角∠β.
(2)作∠MBN=∠β.
(3)在射线BM上截取BC=a.
(4)过点C作CA⊥BM,交BN于点A,如图(2).
△ABC就是所求的直角三角形...
见解析
【解析】试题分析:根据题意写出已知和求作,然后再画出图形即可.
试题解析:已知:线段a和∠α,如下图(1).
求作:Rt△ABC,使BC=a,∠C=90?,∠A=∠α.
作法:(1)作∠α的余角∠β.
(2)作∠MBN=∠β.
(3)在射线BM上截取BC=a.
(4)过点C作CA⊥BM,交BN于点A,如图(2).
△ABC就是所求的直角三角形... 已知二次函数的图象以A(-1,4)为顶点,且过点B(2,-5).
(1)求该二次函数的解析式;
(2)求该二次函数图象与坐标轴的交点坐标;
 (1)二次函数的关系式是y=-(x+1)2+4;(2)交点坐标是(-3,0)、(1,0)
【解析】试题分析:
(1)由题意可设二次函数解析式为,代入点B的坐标(2,-5)求出的值,即可得到二次函数的解析式;
(2)在(1)中所求函数解析式中,由时,求得对应的函数值即可得到函数图象与轴的交点坐标;由可得一元二次方程,解方程即可求得二次函数的图象与轴的交点坐标.
试题解析:
...
(1)二次函数的关系式是y=-(x+1)2+4;(2)交点坐标是(-3,0)、(1,0)
【解析】试题分析:
(1)由题意可设二次函数解析式为,代入点B的坐标(2,-5)求出的值,即可得到二次函数的解析式;
(2)在(1)中所求函数解析式中,由时,求得对应的函数值即可得到函数图象与轴的交点坐标;由可得一元二次方程,解方程即可求得二次函数的图象与轴的交点坐标.
试题解析:
... 若将抛物线y=2x2向上平移3个单位,所得抛物线的解析式为( )
A.y=2x2+3 B.y=2x2﹣3 C.y=2(x﹣3)2 D.y=2(x+3)2
 A.
【解析】
试题分析:由“上加下减”的原则可知,将二次函数y=2x2向上平移3个单位可得到函数y=2x2+3,
故选:A.
A.
【解析】
试题分析:由“上加下减”的原则可知,将二次函数y=2x2向上平移3个单位可得到函数y=2x2+3,
故选:A. 在第一象限内作射线OC,与x轴的夹角为60°,在射线OC上取一点A,过点A作AH⊥x 轴于点H,在抛物线y=x2(x>0)上取一点P,在y轴上取一点Q,使得以P、O、Q为顶点的三角形与△AOH全等,则符合条件的点A的坐标是______.
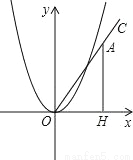
 【解析】试题解析:①如图1,当∠POQ=∠OAH=30°,若以P,O,Q为顶点的三角形与△AOH全等,那么A、P重合;
∵∠AOH=60°,
∴直线OA:y=x,
联立抛物线的解析式得: ,
解得: 或,
故A(,3);
②当∠POQ=∠AOH=60°,此时△POQ≌△AOH,
易知∠POH=30°,则直线y=x,联立抛物线的解析式,得: ,
解得:...
【解析】试题解析:①如图1,当∠POQ=∠OAH=30°,若以P,O,Q为顶点的三角形与△AOH全等,那么A、P重合;
∵∠AOH=60°,
∴直线OA:y=x,
联立抛物线的解析式得: ,
解得: 或,
故A(,3);
②当∠POQ=∠AOH=60°,此时△POQ≌△AOH,
易知∠POH=30°,则直线y=x,联立抛物线的解析式,得: ,
解得:... 若二次函数y=ax2-2ax+c的图象经过点(-1,0),则方程ax2-2ax+c=0的解为 ( )
A. x1=-3,x2=-1 B. x1=1,x2=3 C. x1=-1,x2=3 D. x1=-3,x2=1
 C
【解析】试题分析:根据题意可得:二次函数的对称轴为直线x=1,则函数与x轴的交点坐标为(-1,0)和(3,0),则方程的解为x=-1或x=3.
C
【解析】试题分析:根据题意可得:二次函数的对称轴为直线x=1,则函数与x轴的交点坐标为(-1,0)和(3,0),则方程的解为x=-1或x=3. 阅读下列材料:
解答“已知 ,试确定
,试确定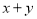 的取值范围”有如下解法:
的取值范围”有如下解法:
【解析】
∵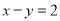 ,∴x=y+2,又∵
,∴x=y+2,又∵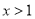 ,∴
,∴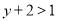 ,即
,即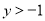
又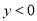 ,∴
,∴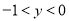 .…①
.…①
同理得: 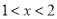 .…②
.…②
由①+②得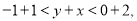
∴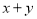 的取值范围是
的取值范围是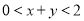 .
.
请按照上述方法,完成下列问题 :
已知关于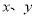 的方程组
的方程组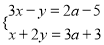 的解都是正数.
的解都是正数.
(1)求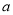 的取值范围;
的取值范围;
(2)已知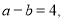 且
且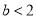 ,求
,求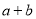 的取值范围;
的取值范围;
(3) 已知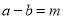 (
(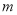 是大于0的常数),且
是大于0的常数),且 的最大值.(用
的最大值.(用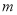 含的式子表示)
含的式子表示)
 (1);(2)(3)
【解析】(1 ) x=a-1, y=a+2(2分) (3分)
(2) 1
(1);(2)(3)
【解析】(1 ) x=a-1, y=a+2(2分) (3分)
(2) 1如图所示,E,F分别为平行四边形ABCD中AD,BC的中点,G,H在BD上,且 BG=DH,求证四边形EGFH是平行四边形.
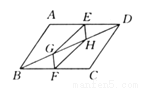
 答案见解析
【解析】试题分析:由四边形ABCD是平行四边形,得到AD=BC,AD∥BC,由AD∥BC,得到∠ADB=∠DBC,因为E、F分别为?ABCD的边AD、BC的中点,得到DE=BF,由三角形全等证得EH=FG,∠EHD=∠FGB,得到EH∥FG,证出四边形FGEH是平行四边形.
试题解析:证明:∵四边形ABCD是平行四边形,∴AD=BC,AD∥BC,∴∠ADB=∠DBC.∵E、...
答案见解析
【解析】试题分析:由四边形ABCD是平行四边形,得到AD=BC,AD∥BC,由AD∥BC,得到∠ADB=∠DBC,因为E、F分别为?ABCD的边AD、BC的中点,得到DE=BF,由三角形全等证得EH=FG,∠EHD=∠FGB,得到EH∥FG,证出四边形FGEH是平行四边形.
试题解析:证明:∵四边形ABCD是平行四边形,∴AD=BC,AD∥BC,∴∠ADB=∠DBC.∵E、... 下列条件中,能判别四边形是平行四边形的是 ( )
A. 一组对边相等,另一组对边平行 B. 一组对边平行,一组对角互补
C. 一组对角相等,一组邻角互补 D. 一组对角互补,另一组对角相等
 C
【解析】解:A.一组对边相等,另一组对边平行,也有可能是等腰梯形;
B.一组对边平行,一组对角互补,也有可能是等腰梯形;
C.一组对角相等,一组邻角互补可得到两组对角分别相等,所以是平行四边形;
D.一组对角互补,另一组对角相等,可能是含两个直角的一般四边形.
故选C.
C
【解析】解:A.一组对边相等,另一组对边平行,也有可能是等腰梯形;
B.一组对边平行,一组对角互补,也有可能是等腰梯形;
C.一组对角相等,一组邻角互补可得到两组对角分别相等,所以是平行四边形;
D.一组对角互补,另一组对角相等,可能是含两个直角的一般四边形.
故选C. 
