题目内容
13.设m,n都是有理数,且$\sqrt{9}$-$\sqrt{32}$+$\sqrt{\frac{1}{8}}$=m+n$\sqrt{2}$,求m,n的值.分析 先将$\sqrt{9}$-$\sqrt{32}$+$\sqrt{\frac{1}{8}}$=m+n$\sqrt{2}$变形为3-4$\sqrt{2}$+$\frac{\sqrt{2}}{4}$=m+n$\sqrt{2}$,即3-$\frac{15\sqrt{2}}{4}$=m+n$\sqrt{2}$,再根据m,n都是有理数得到关于m,n的方程即可求解.
解答 解:$\sqrt{9}$-$\sqrt{32}$+$\sqrt{\frac{1}{8}}$=m+n$\sqrt{2}$,
3-4$\sqrt{2}$+$\frac{\sqrt{2}}{4}$=m+n$\sqrt{2}$,即3-$\frac{15\sqrt{2}}{4}$=m+n$\sqrt{2}$,
则m=3,n=-$\frac{15}{4}$.
点评 此题考查了算术平方根,熟练掌握运算法则是解本题的关键.

练习册系列答案
 励耘书业暑假衔接宁波出版社系列答案
励耘书业暑假衔接宁波出版社系列答案
相关题目
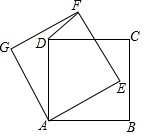 如图,正方形AEFG和正方形ABCD是两个全等的正方形,若∠EAB=30°,求∠DFE的大小.
如图,正方形AEFG和正方形ABCD是两个全等的正方形,若∠EAB=30°,求∠DFE的大小.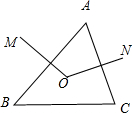 如图,在△ABC中,OM、ON分别是AB、AC的垂直平分线,OM与ON相交于点O.求证:点O在BC的垂直平分线上.
如图,在△ABC中,OM、ON分别是AB、AC的垂直平分线,OM与ON相交于点O.求证:点O在BC的垂直平分线上.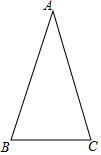 如图,△ABC是等腰三角形,AB=AC,∠A=36°.
如图,△ABC是等腰三角形,AB=AC,∠A=36°.