题目内容
8.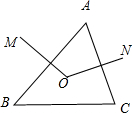 如图,在△ABC中,OM、ON分别是AB、AC的垂直平分线,OM与ON相交于点O.求证:点O在BC的垂直平分线上.
如图,在△ABC中,OM、ON分别是AB、AC的垂直平分线,OM与ON相交于点O.求证:点O在BC的垂直平分线上.
分析 连接AO、BO、CO,根据线段垂直平分线上任意一点,到线段两端点的距离相等可得AO=BO,AO=CO,利用等量代换可得CO=BO,再根据到线段两端点的距离相等的点在线段的垂直平分线上可得结论.
解答  证明:连接AO、BO、CO,
证明:连接AO、BO、CO,
∵OM是AB的垂直平分线,
∴AO=BO,
∵ON分别是AC的垂直平分线,
∴AO=CO,
∴CO=BO,
∴点O在BC的垂直平分线上.
点评 此题主要考查了线段垂直平分线的性质和判定,关键是掌握线段垂直平分线上任意一点,到线段两端点的距离相等;到线段两端点的距离相等的点在线段的垂直平分线上.

练习册系列答案
相关题目
3.下列代数式是最简形式的是( )
| A. | $\frac{{{x^2}-4}}{x-2}$ | B. | $\frac{{4{x^2}+4x+1}}{2x+1}$ | C. | $\sqrt{4{x^3}}$ | D. | $\frac{{\sqrt{5}-1}}{2}$ |
18.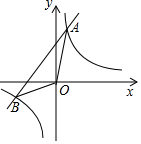 如图,点A、B是双曲线y=$\frac{k+1}{x}$(k为正整数)与直线AB的交点,且A、B两点的横坐标是关于x的方程:x2+kx-k-1=0的两根
如图,点A、B是双曲线y=$\frac{k+1}{x}$(k为正整数)与直线AB的交点,且A、B两点的横坐标是关于x的方程:x2+kx-k-1=0的两根
(1)填表:
(2)当k=n(n为正整数)时,试求直线AB的解析式(用含n的式子表示);
(3)当k=1、2、3、…n时,△ABO的面积,依次记为S1、S2、S3…Sn,当Sn=40时,求双曲线y=$\frac{k+1}{x}$的解析式.
 如图,点A、B是双曲线y=$\frac{k+1}{x}$(k为正整数)与直线AB的交点,且A、B两点的横坐标是关于x的方程:x2+kx-k-1=0的两根
如图,点A、B是双曲线y=$\frac{k+1}{x}$(k为正整数)与直线AB的交点,且A、B两点的横坐标是关于x的方程:x2+kx-k-1=0的两根(1)填表:
| K | 1 | 2 | 3 | … | n(n为正整数) |
| A点的横坐标 | 1 | 1 | 1 | … | 1 |
| B点的横坐标 | -2 | -3 | -4 | … | -n-1 |
(3)当k=1、2、3、…n时,△ABO的面积,依次记为S1、S2、S3…Sn,当Sn=40时,求双曲线y=$\frac{k+1}{x}$的解析式.
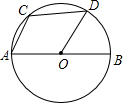 如图,已知AB是⊙O的直径,弦AC与半径OD平行.
如图,已知AB是⊙O的直径,弦AC与半径OD平行.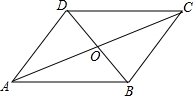 己知如图,在平行四边形ABCD中,AC=$\sqrt{2}$AB,求证:△AOB∽△ABC.
己知如图,在平行四边形ABCD中,AC=$\sqrt{2}$AB,求证:△AOB∽△ABC.