题目内容
2.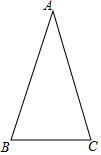 如图,△ABC是等腰三角形,AB=AC,∠A=36°.
如图,△ABC是等腰三角形,AB=AC,∠A=36°.(1)利用尺规作∠B的角平分线BD,交AC于点D;(保留作图痕迹,不写作法)
(2)求∠BDC的度数?
分析 (1)首先以B为圆心,任意长为半径画弧,分别交AB、BC两点,然后以这两个交点为圆心,大于两个交点之间的距离的一半为半径画弧,两弧的交点为P,最后画射线BP即可求解;
(2)由∠A=36°,求出∠C、∠ABC的度数,能求出∠ABD和∠CBD的度数,即可求出∠BDC.
解答 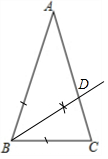 解:(1)如图,射线BD即为所求;
解:(1)如图,射线BD即为所求;
(2)∵AB=AC,∠A=36°
∴∠ABC=∠C=72°,
∵BD平分∠ABC,
∴∠DBC=$\frac{1}{2}$∠ABC=36°,
∴∠BDC=∠C=72°.
点评 本题主要考查了等腰三角形的性质和判定,三角形的内角和定理,角平分线的性质,作图与基本作图等知识点,解此题的关键是能正确画图和求出∠C、∠BDC的度数.

练习册系列答案
 黄冈小状元同步计算天天练系列答案
黄冈小状元同步计算天天练系列答案
相关题目
11.一元二次方程x2-6x-10=0配方后可变形为( )
| A. | (x-3)2=19 | B. | (x-3)2=1 | C. | (x+3)2=19 | D. | (x+3)2=1 |
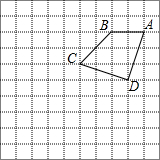 如图,在正方形网格图中,点A、B、C、D均在格点上,以点A为位似中心,将四边形ABCD放大到原来的2倍得到四边形AB′C′D′.
如图,在正方形网格图中,点A、B、C、D均在格点上,以点A为位似中心,将四边形ABCD放大到原来的2倍得到四边形AB′C′D′.