题目内容
1.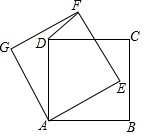 如图,正方形AEFG和正方形ABCD是两个全等的正方形,若∠EAB=30°,求∠DFE的大小.
如图,正方形AEFG和正方形ABCD是两个全等的正方形,若∠EAB=30°,求∠DFE的大小.
分析 连接DE.只要证明△ADE是等边三角形,推出∠AED=60°,推出ED=EF,∠FED=30°.
解答  解:连接DE.
解:连接DE.
∵正方形AEFG和正方形ABCD是两个全等的正方形,
∴AD=AE,∠DAB=∠AEF=90°,
∵∠EAB=30°,
∴△ADE是等边三角形,
∴∠DEA=60°,DE=AE=EF,
∴∠DEF=30°,
∴∠DFE=∠EDF=75°.
点评 本题考查正方形的性质、等边三角形的判定和性质、等腰三角形的性质等知识,解题的关键是证明△AED是等边三角形,属于中考常考题型.

练习册系列答案
相关题目
11.一元二次方程x2-6x-10=0配方后可变形为( )
| A. | (x-3)2=19 | B. | (x-3)2=1 | C. | (x+3)2=19 | D. | (x+3)2=1 |

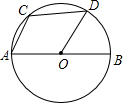 如图,已知AB是⊙O的直径,弦AC与半径OD平行.
如图,已知AB是⊙O的直径,弦AC与半径OD平行.