题目内容
3．解方程：$\frac{2x-3}{6}$-$\frac{3x-2}{4}$=1．分析 方程去分母，去括号，移项合并，把x系数化为1，即可求出解．
解答 解：去分母得：4x-6-9x+6=12，
移项合并得：-5x=12，
解得：x=-2.4．
点评 此题考查了解一元一次方程，解方程去分母时注意各项都乘以各分母的最小公倍数．
练习册系列答案
相关题目
11．一元二次方程x2-6x-10=0配方后可变形为（ ）
| A． | （x-3）2=19 | B． | （x-3）2=1 | C． | （x+3）2=19 | D． | （x+3）2=1 |
18．
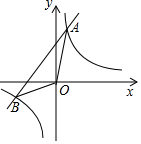如图，点A、B是双曲线y=$\frac{k+1}{x}$（k为正整数）与直线AB的交点，且A、B两点的横坐标是关于x的方程：x2+kx-k-1=0的两根
（1）填表：
（2）当k=n（n为正整数）时，试求直线AB的解析式（用含n的式子表示）；
（3）当k=1、2、3、…n时，△ABO的面积，依次记为S1、S2、S3…Sn，当Sn=40时，求双曲线y=$\frac{k+1}{x}$的解析式．
如图，点A、B是双曲线y=$\frac{k+1}{x}$（k为正整数）与直线AB的交点，且A、B两点的横坐标是关于x的方程：x2+kx-k-1=0的两根（1）填表：
| K | 1 | 2 | 3 | … | n（n为正整数） |
| A点的横坐标 | 1 | 1 | 1 | … | 1 |
| B点的横坐标 | -2 | -3 | -4 | … | -n-1 |
（3）当k=1、2、3、…n时，△ABO的面积，依次记为S1、S2、S3…Sn，当Sn=40时，求双曲线y=$\frac{k+1}{x}$的解析式．
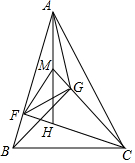如图，△ABC为锐角三角形，CF⊥AB于F，H为△ABC的垂心．M为AH的中点，点G在线段CM上，且CG⊥GB．