题目内容
1.已知:如图,在△ABC中,点A1、B1、C1分别是BC、AC、AB的中点,A2、B2、C2分别是B1C1、A1C1、A1B1的中点,以此类推…,若△ABC的周长为1,则△A2015B2015C2015的周长为$\frac{1}{{2}^{2015}}$.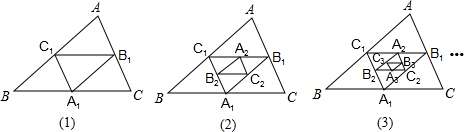
分析 由三角形的中位线定理得:A1B1、B1C1、C1A1分别等于BC、CA、AB的一半,所以△A1B1C1的周长等于△ABC的周长的一半,以此类推可求出△A2015B2015C2015的周长.
解答 解:∵A1、B1、C1分别为BC、CA、AB的中点,
∴A1B1、B1C1、C1A1分别等于BC、CA、AB的$\frac{1}{2}$,
∵A2、B2、C2分别为B1C1、C1A1、A1B1的中点,
∴B1C1、C1A1、A1B1分别为A1B1、B1C1、C1A1的$\frac{1}{2}$,
∴以此类推:△A4B4C4的周长为△ABC的周长的$\frac{1}{2}$,
∴△A2015B2015C2015=$\frac{1}{{2}^{2015}}$×1=$\frac{1}{{2}^{2015}}$.
则故答案为:$\frac{1}{{2}^{2015}}$.
点评 本题考查了三角形的中位线定理,中位线是三角形中的一条重要线段,由于它的性质与线段的中点及平行线紧密相连,因此,它在几何图形的计算及证明中有着广泛的应用.

练习册系列答案
 期末好成绩系列答案
期末好成绩系列答案 99加1领先期末特训卷系列答案
99加1领先期末特训卷系列答案 百强名校期末冲刺100分系列答案
百强名校期末冲刺100分系列答案 好成绩1加1期末冲刺100分系列答案
好成绩1加1期末冲刺100分系列答案 金状元绩优好卷系列答案
金状元绩优好卷系列答案
相关题目
9.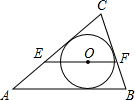 如图,O是△ABC的内心,过点O作EF∥AB,分别交AC、BC于点E、F,则( )
如图,O是△ABC的内心,过点O作EF∥AB,分别交AC、BC于点E、F,则( )
 如图,O是△ABC的内心,过点O作EF∥AB,分别交AC、BC于点E、F,则( )
如图,O是△ABC的内心,过点O作EF∥AB,分别交AC、BC于点E、F,则( )| A. | EF>AE+BF | B. | EF<AE+BF | C. | EF2=AE•BF | D. | EF=AE+BF |
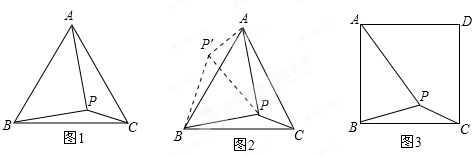
 已知点C是线段AB延长线上一点,M为AC的中点,N为BC的中点,若AB=8,求MN的长.
已知点C是线段AB延长线上一点,M为AC的中点,N为BC的中点,若AB=8,求MN的长.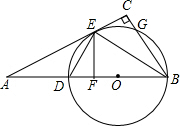 如图,在△ABC中,∠C=90°,BE是∠ABC的平分线,过点E作BE的垂线交AB于点F,⊙O是△BDE的外接圆.求证:
如图,在△ABC中,∠C=90°,BE是∠ABC的平分线,过点E作BE的垂线交AB于点F,⊙O是△BDE的外接圆.求证: