题目内容
17.已知某一铁路隧道长1500米.有一列火车匀速从隧道通过,测得火车开始进入隧道到完全出隧道共有1分钟,整列火车都在隧道里的时间为40秒,设火车长x米,火车的速度y米/秒,则可得方程组( )| A. | $\left\{\begin{array}{l}1500+2x=60y\\ 1500-2x=40y\end{array}\right.$ | B. | $\left\{\begin{array}{l}1500+x=60y\\ 1500-x=40y\end{array}\right.$ | ||
| C. | $\left\{\begin{array}{l}1500+x=60y\\ 1500-2x=40y\end{array}\right.$ | D. | $\left\{\begin{array}{l}1500+2x=60y\\ 1500-x=40y\end{array}\right.$ |
分析 通过理解题意可知本题存在两个等量关系,即整列火车过桥通过的路程=桥长+车长,整列火车在桥上通过的路程=桥长-车长,根据这两个等量关系可列出方程组求解.
解答 解:设火车的速度为每秒x米,车长为y米,由题意得
$\left\{\begin{array}{l}{60y=1500+x}\\{40y=1500-x}\end{array}\right.$,
故选:B.
点评 此题考查由实际问题抽象出二元一次方程组,解题关键是弄清题意,合适的等量关系,列出方程组.弄清桥长、车长以及整列火车过桥通过的路程,整列火车在桥上通过的路程之间的关系.

练习册系列答案
 手拉手全优练考卷系列答案
手拉手全优练考卷系列答案
相关题目
5.若分式$\frac{x}{x-3}$有意义,则x应满足的条件是( )
| A. | x≠3 | B. | x<3 | C. | x≠3且x≠0 | D. | x≠0 |
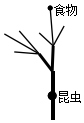 一只昆虫在如图所示的树枝上寻觅食物,假定昆虫在每个岔路口都会随机地选择一条路径,则它获得食物的概率是$\frac{1}{6}$.
一只昆虫在如图所示的树枝上寻觅食物,假定昆虫在每个岔路口都会随机地选择一条路径,则它获得食物的概率是$\frac{1}{6}$.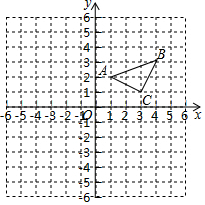 如图所示,三角形ABC三个顶点A、B、C的坐标分别为A (1,2)、B(4,3)、C(3,1).
如图所示,三角形ABC三个顶点A、B、C的坐标分别为A (1,2)、B(4,3)、C(3,1). 的图象如图所示,则反比例函数
的图象如图所示,则反比例函数 与一次函数
与一次函数 在同一坐标系中的大致图象是
在同一坐标系中的大致图象是
 B.
B.  C.
C.  D.
D.