题目内容
2.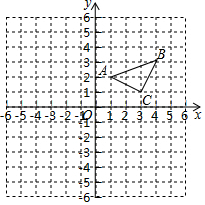 如图所示,三角形ABC三个顶点A、B、C的坐标分别为A (1,2)、B(4,3)、C(3,1).
如图所示,三角形ABC三个顶点A、B、C的坐标分别为A (1,2)、B(4,3)、C(3,1).(1)将△ABC先向右平移2个单位长度,再向下平移3个单位长度,得到△A'B'C',则A'B'C'的三个顶点坐标分别是A'(3、-1)、
B'(6、0)、C'(5、-2);
(2)画出平移后的图形.
(3)求△ABC的面积.(本小题必须写出解答过程)
分析 (1)根据点的平移规律解答即可得;
(2)将(1)中所得点顺次连接即可得;
(3)割补法求解可得.
解答 解:(1)将△ABC先向右平移2个单位长度,再向下平移3个单位长度,得到△A'B'C',
则△A'B'C'的三个顶点坐标分别是A'(3,-1)、B′(6,0)、C′(5,-2),
故答案为:3,-1,6,0,5,-2;
(2)如下图,△A'B'C'即为所求:
(3)S△ABC=2×3-$\frac{1}{2}$×1×3-$\frac{1}{2}$×1×2-$\frac{1}{2}$×1×2=$\frac{5}{2}$.
点评 本题考查的是作图-平移变换,熟知图形平移不变性的性质是解答此题的关键.

练习册系列答案
 活力课时同步练习册系列答案
活力课时同步练习册系列答案
相关题目
10.若多项式x2-(x-a)(x+2b)+4的值与x的取值大小无关,那么a,b一定满足( )
| A. | a=0且b=0 | B. | a=2b | C. | ab=0 | D. | $a=\frac{b}{2}$ |
17.已知某一铁路隧道长1500米.有一列火车匀速从隧道通过,测得火车开始进入隧道到完全出隧道共有1分钟,整列火车都在隧道里的时间为40秒,设火车长x米,火车的速度y米/秒,则可得方程组( )
| A. | $\left\{\begin{array}{l}1500+2x=60y\\ 1500-2x=40y\end{array}\right.$ | B. | $\left\{\begin{array}{l}1500+x=60y\\ 1500-x=40y\end{array}\right.$ | ||
| C. | $\left\{\begin{array}{l}1500+x=60y\\ 1500-2x=40y\end{array}\right.$ | D. | $\left\{\begin{array}{l}1500+2x=60y\\ 1500-x=40y\end{array}\right.$ |
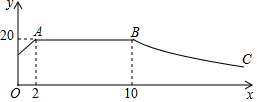 我市某蔬菜生产基地在气温较低时,用装有恒温系统的大棚栽培一种在自然光照且大棚内温度为20℃的条件下生长最快的新品种,如图是某天恒温系统从开启到关闭及关闭后大棚内温度y(单位:℃)随光照时间x(单位:h)变化的大致图象,其中BC段是双曲线y=$\frac{k}{x}$的一部分.请根据图中信息解答下列问题:
我市某蔬菜生产基地在气温较低时,用装有恒温系统的大棚栽培一种在自然光照且大棚内温度为20℃的条件下生长最快的新品种,如图是某天恒温系统从开启到关闭及关闭后大棚内温度y(单位:℃)随光照时间x(单位:h)变化的大致图象,其中BC段是双曲线y=$\frac{k}{x}$的一部分.请根据图中信息解答下列问题:

