题目内容
18. 快、慢两车分别从相距480km的甲,乙两地同时出发,匀速行驶,相向而行,途中慢车因故停留了1小时,然后继续以原速驶向甲地,到达甲地后即停止行驶;快车到达乙地后,立即按原路原速返回甲地(调头时间忽略不计).如图是快、慢两车距乙地路程y(km)与所用时间x(h)之间的函数图象,则当两车第一次相遇时,快车距离甲地的路程是320千米.
快、慢两车分别从相距480km的甲,乙两地同时出发,匀速行驶,相向而行,途中慢车因故停留了1小时,然后继续以原速驶向甲地,到达甲地后即停止行驶;快车到达乙地后,立即按原路原速返回甲地(调头时间忽略不计).如图是快、慢两车距乙地路程y(km)与所用时间x(h)之间的函数图象,则当两车第一次相遇时,快车距离甲地的路程是320千米.
分析 根据行程问题的数量关系:速度=路程÷时间及路程=速度×时间就可以得出:乙的速度和a的值,所以可求出点D的坐标,再由题意可以求出快车的速度就可以求出点B的坐标,由待定系数法求出AB的解析式及OD的解析式就可以求出结论.
解答 解:由题意,得慢车的速度为:480÷(9-1)=60千米/时,
∴a=60×(7-1)=360.
则5×60=300,
∴D(5,300),
设yOD=k1x,由题意,得
300=5k1,
∴k1=60,
∴yOD=60x.
∵快车的速度为:(480+360)÷7=120千米/时.
∴480÷120=4小时.
∴B(4,0),C(8,480).
设yAB=k2x+b,由题意,得
$\left\{\begin{array}{l}{4{k}_{2}+b=0}\\{b=480}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{{k}_{2}=-120}\\{b=480}\end{array}\right.$,
∴yAB=-120x+480
∴$\left\{\begin{array}{l}{y=60x}\\{y=-120x+480}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{x=\frac{8}{3}}\\{y=160}\end{array}\right.$.
∴480-160=320千米.
答:快车与慢车第一次相遇时,距离甲地的路程是320千米;
故答案为:320.
点评 本题考查了行程问题的数量关系路程=速度×时间的运用,待定系数法求一次函数的解析式的运用,一次函数与一元一次方程的关系的运用,解答时求出一次函数的解析式是关键.

练习册系列答案
 阳光课堂课时作业系列答案
阳光课堂课时作业系列答案
相关题目
13.某射击队教练为了了解队员训练情况,从队员中选取甲、乙两名队员进行射击测试,相同条件下各射靶5次,成绩统计如下:
(1)根据上述信息可知:甲命中环数的中位数是8环,乙命中环数的众数是6和9环;
(2)试通过计算说明甲、乙两人的成绩谁比较稳定?
(3)如果乙再射击1次,命中8环,那么乙射击成绩的方差会变小.(填“变大”、“变小”或“不变”)
| 命中环数 | 6 | 7 | 8 | 9 | 10 |
| 甲命中相应环数的次数 | 0 | 1 | 3 | 1 | 0 |
| 乙命中相应环数的次数 | 2 | 0 | 0 | 2 | 1 |
(2)试通过计算说明甲、乙两人的成绩谁比较稳定?
(3)如果乙再射击1次,命中8环,那么乙射击成绩的方差会变小.(填“变大”、“变小”或“不变”)
2.三边长均为整数且周长为12的三角形的个数为( )
| A. | 2个 | B. | 3个 | C. | 4个 | D. | 5个 |
 如图,⊙O为△ABC的外接圆,其中D点在$\widehat{AC}$上,且OD⊥AC,已知∠A=36°,∠C=60°,则∠BOD=156°.
如图,⊙O为△ABC的外接圆,其中D点在$\widehat{AC}$上,且OD⊥AC,已知∠A=36°,∠C=60°,则∠BOD=156°.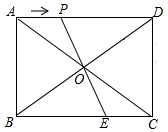 如图,在矩形ABCD中,AB=6cm,BC=8cm,对角线AC,BD交于点O,点P从点A出发,沿AD方向匀速运动,速度为2cm/s,当OD平分∠COP时,运动时间为$\frac{56}{39}$s.
如图,在矩形ABCD中,AB=6cm,BC=8cm,对角线AC,BD交于点O,点P从点A出发,沿AD方向匀速运动,速度为2cm/s,当OD平分∠COP时,运动时间为$\frac{56}{39}$s.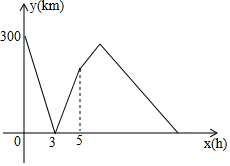 甲,乙两车分别从A,B两地同时相向匀速行驶,乙车到达A地后未作停留,继续保持原速向远离B地的方向行驶,而甲车到达B地后修整了1个小时,然后调头并保持原速与乙车同向行驶,经过一段时间后两车同时到达C地.设两车行驶的时间为x(小时),两车之间的距离为y(千米),y与x之间的函数图象如图所示,则A,C两地相距420千米.
甲,乙两车分别从A,B两地同时相向匀速行驶,乙车到达A地后未作停留,继续保持原速向远离B地的方向行驶,而甲车到达B地后修整了1个小时,然后调头并保持原速与乙车同向行驶,经过一段时间后两车同时到达C地.设两车行驶的时间为x(小时),两车之间的距离为y(千米),y与x之间的函数图象如图所示,则A,C两地相距420千米.