题目内容
在等腰梯形ABCD中，AB∥DC，AD=BC．若∠D=105°，对角线AC⊥BD，则tan∠DAC= ．
考点：等腰梯形的性质
专题：
分析：过C点作DB的平行线，交AB延长线与E，因为AC⊥BD，所以AC⊥CE，因为AB∥CD，DB∥CE所以DB=CE，所以AC=CE，所以∠CAD为45°，因为∠ADC为105°∠DAC为30度，进而可求出tan∠DAC的值．
解答：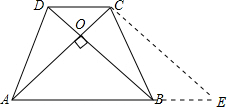
解：过C点作DB的平行线，交AB延长线与E，
∵AC⊥BD，
∴AC⊥CE，
∵AB∥CD，DB∥CE
∴DB=CE，
∴AC=CE，
∴∠CAD为45°，
∵∠ADC=105°，
∴∠DAC=30°，
∴tan∠DAC=
，
故答案为：
．
解：过C点作DB的平行线，交AB延长线与E，∵AC⊥BD，
∴AC⊥CE，
∵AB∥CD，DB∥CE
∴DB=CE，
∴AC=CE，
∴∠CAD为45°，
∵∠ADC=105°，
∴∠DAC=30°，
∴tan∠DAC=
| ||
| 3 |
故答案为：
| ||
| 3 |
点评：本题主要考查对平行线的性质，等腰直角三角形的性质，平行四边形的性质和判定，等腰梯形的性质等知识点的理解和掌握，能把梯形转化成平行四边形和等腰三角形是解此题的关键．
练习册系列答案
相关题目
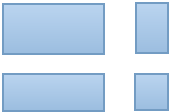如图，在一块长为22米，宽为17米的矩形地面上，要修建同样宽的两条互相垂直的道路（两条道路各与矩形的一条边平行），剩余部分种上草坪，使草坪面积为300平方米，那么道路的宽度应该是多少？最小两位数与最大两位数的和是（ ）
| A、109 | B、110 |
| C、0 | D、101 |