题目内容
13.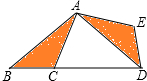 如图所示,在△ABC中,∠B=40°,将△ABC绕点A逆时针旋转至△ADE处,使点B落在BC延长线上的D点处,则旋转角∠BAD=100度.
如图所示,在△ABC中,∠B=40°,将△ABC绕点A逆时针旋转至△ADE处,使点B落在BC延长线上的D点处,则旋转角∠BAD=100度.
分析 根据旋转的性质得AB=AD,∠BAD等于旋转角,再根据等腰三角形的性质得∠B=∠ADB=40°,然后根据三角形内角和定理计算∠BAD的度数.
解答 解:∵△ABC绕点A逆时针旋转至△ADE处,使点B落在BC延长线上的D点处,
∴AB=AD,∠BAD等于旋转角,
∴∠B=∠ADB=40°,
∴∠BAD=180°-∠B-∠ADB=100°.
故答案为100.
点评 本题考查了旋转的性质:对应点到旋转中心的距离相等;对应点与旋转中心所连线段的夹角等于旋转角;旋转前、后的图形全等.

练习册系列答案
相关题目
1.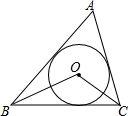 如图,已知⊙O是△ABC的内切圆,且∠ABC=50°,∠ACB=80°,则∠BOC=( )
如图,已知⊙O是△ABC的内切圆,且∠ABC=50°,∠ACB=80°,则∠BOC=( )
 如图,已知⊙O是△ABC的内切圆,且∠ABC=50°,∠ACB=80°,则∠BOC=( )
如图,已知⊙O是△ABC的内切圆,且∠ABC=50°,∠ACB=80°,则∠BOC=( )| A. | 100° | B. | 75° | C. | 115° | D. | 105° |
2.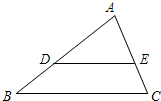 如图,△ABC中,DE∥BC,AD:DB=2:1,则△ADE与△ABC的面积之比是( )
如图,△ABC中,DE∥BC,AD:DB=2:1,则△ADE与△ABC的面积之比是( )
 如图,△ABC中,DE∥BC,AD:DB=2:1,则△ADE与△ABC的面积之比是( )
如图,△ABC中,DE∥BC,AD:DB=2:1,则△ADE与△ABC的面积之比是( )| A. | 4:1 | B. | 8:1 | C. | 4:9 | D. | 2:3 |
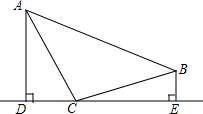 如图,点C在DE上,AC=BC,AD⊥DE于D,BE⊥DE于E,AD=CE.求证:AC⊥BC.
如图,点C在DE上,AC=BC,AD⊥DE于D,BE⊥DE于E,AD=CE.求证:AC⊥BC. 如图,△ABC中,AB=AC,∠B=70°.
如图,△ABC中,AB=AC,∠B=70°.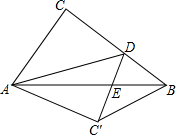 如图,在Rt△ABC中,∠ACB=90°,AB=5,AC=3,点D是BC上一动点,连结AD,将△ACD沿AD折叠,点C落在点C′,连结C′D交AB于点E,连结BC′.当△BC′D是直角三角形时,DE的长为$\frac{3}{2}$或$\frac{3}{4}$.
如图,在Rt△ABC中,∠ACB=90°,AB=5,AC=3,点D是BC上一动点,连结AD,将△ACD沿AD折叠,点C落在点C′,连结C′D交AB于点E,连结BC′.当△BC′D是直角三角形时,DE的长为$\frac{3}{2}$或$\frac{3}{4}$. 一个几何体,是由许多规格相同的小正方体堆积而成的,从正面看和从左面看的形状如图所示,要搭成这样的几何体,最少需用6块小正方体.
一个几何体,是由许多规格相同的小正方体堆积而成的,从正面看和从左面看的形状如图所示,要搭成这样的几何体,最少需用6块小正方体.