题目内容
4.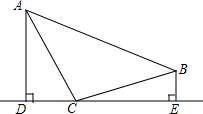 如图,点C在DE上,AC=BC,AD⊥DE于D,BE⊥DE于E,AD=CE.求证:AC⊥BC.
如图,点C在DE上,AC=BC,AD⊥DE于D,BE⊥DE于E,AD=CE.求证:AC⊥BC.
分析 根据已知条件从而可以求出△ACD≌△CBE,进而证明即可.
解答 证明:∵AD⊥DE于D,BE⊥DE于E,
在Rt△ACD与Rt△CBE中,
$\left\{\begin{array}{l}{AC=BC}\\{AD=CE}\end{array}\right.$,
∴Rt△ACD≌Rt△CBE(HL),
∴∠ACD=∠CBE,
∵∠CBE++∠BCE=90°,
∴∠ACD+∠BCE=90°,
∴∠ACB=90°,
∴AC⊥BC.
点评 本题考查了直角三角形的有关知识以及三角形全等的有关知识,关键是根据已知条件从而可以求出△ACD≌△CBE.

练习册系列答案
 七星图书口算速算天天练系列答案
七星图书口算速算天天练系列答案
相关题目
19.某摩托车厂本周计划每日生产250辆摩托车,由于工人实行轮休,每日上班人数不一定相等,实际每日产量与计划产量相比情况如下:
(1)本周六生产了多少辆?
(2)本周生产总量与计划生产量相比是增产还是减产?增产或减产几辆?
(3)产量最多的一天比产量最少的一天多生产多少辆?
| 星 期 | 一 | 二 | 三 | 四 | 五 | 六 | 日 |
| 增 减 | -5 | +10 | -3 | +4 | +6 | -8 | -6 |
(2)本周生产总量与计划生产量相比是增产还是减产?增产或减产几辆?
(3)产量最多的一天比产量最少的一天多生产多少辆?
9.若x2+8x+m是完全平方式,则m的值等于( )
| A. | 16 | B. | 8 | C. | 4 | D. | 1 |
 在平面直角坐标系中,一次函数的图象与坐标轴围成的三角形,叫做此一次函数的坐标三角形.例如,图中的一次函数的图象与x,y轴分别交于点A,B,则△OAB为此函数的坐标三角形.
在平面直角坐标系中,一次函数的图象与坐标轴围成的三角形,叫做此一次函数的坐标三角形.例如,图中的一次函数的图象与x,y轴分别交于点A,B,则△OAB为此函数的坐标三角形.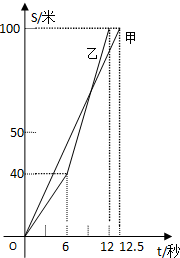 甲、乙两同学在一次百米赛跑中,路程S(米)与时间t(秒)之间的关系如图所示.根据图象回答下列问题:
甲、乙两同学在一次百米赛跑中,路程S(米)与时间t(秒)之间的关系如图所示.根据图象回答下列问题: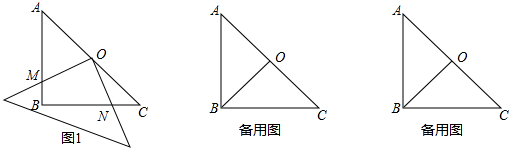
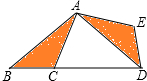 如图所示,在△ABC中,∠B=40°,将△ABC绕点A逆时针旋转至△ADE处,使点B落在BC延长线上的D点处,则旋转角∠BAD=100度.
如图所示,在△ABC中,∠B=40°,将△ABC绕点A逆时针旋转至△ADE处,使点B落在BC延长线上的D点处,则旋转角∠BAD=100度.