题目内容
14．关于x的方程x2+（t-2）x+5-t=0的两个根都大于2，则t的取值范围是-5＜t≤-4．分析 设方程的两根为x1，x2，由关于x的方程x2+（t-2）x+5-t=0的两个根都大于2，得出△≥0且（x1-2）（x2-2）＞0，利用根与系数的关系化简，再解不等式组即可．
解答 解：设关于x的方程x2+（t-2）x+5-t=0的两根为x1，x2，
则x1+x2=2-t，x1x2=5-t．
∵关于x的方程x2+（t-2）x+5-t=0的两个根都大于2，对称轴x=$\frac{b}{-2a}$≥2
∴△=（t-2）2-4（5-t）≥0，且（x1-2）（x2-2）=5-t-2（2-t）+4＞0，且$\frac{2-t}{2}≥2$
解得-5＜t≤-4．
故答案为-5＜t≤-4．
点评 本题考查了根与系数的关系：x1，x2是一元二次方程ax2+bx+c=0（a≠0）的两根时，x1+x2=-$\frac{b}{a}$，x1x2=$\frac{c}{a}$，也考查了根的判别式．
练习册系列答案
相关题目
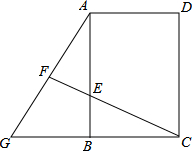如图，点E在矩形ABCD的边AB上，点G在CB的延长线上，连接AG，直线CE交于AG于点F，若AF=GF，∠BCE=30°，EF=4，AE=8，则BC=4$\sqrt{3}$．
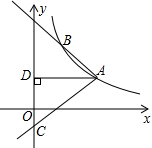如图，反比例函数y=$\frac{k}{x}$（x＞0）的图象经过点A（2$\sqrt{3}$，1），射线AB与反比例函数的图象交于另一点B（1，a），射线AC与y轴交于点C，∠BAC=75°，AD⊥y轴，垂足为D．
一个面积为100cm2的矩形，被分成9个小矩形，现知四个小矩形面积为A=4cm2，B=14cm2，C=3cm2，D=6cm2，求矩形E的面积．